题目内容
2. 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.(1)图出△ABC向左平移4个单位后的图形△A1B1C1;
(2)图中AC与A1C1的关系是:平行且相等
(3)画出△ABC的AB边上的高CD;
(4)能使S△QAB=S△ABC的格点Q(异于点C)的个数有8个;
(5)在直线B1C1上标出点P,使得|PA-PB|的值最大.
分析 (1)将原三角形的三顶点分别向左平移4个单位得到其对应点,顺次连接即可得;
(2)利用平移的性质得出AC与A1C1的关系;
(3)根据三角形高的定义可得;
(4)过点C作平行于AB的直线、再AB的另一侧作直线平行于AB且该直线到AB的距离等于CD,据此可得;
(5)延长BA交直线B1C1于点P,此时|PA-PB|=AB,最大.
解答 解:(1)如图所示,△A1B1C1即为所求;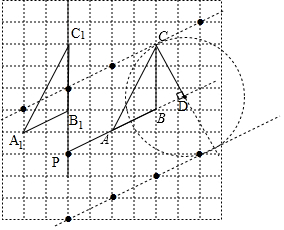
(2)AC与A1C1的关系是:平行且相等,
故答案为:平行且相等;
(3)如图,CD即为所求;
(4)如图,能使S△QAB=S△ABC的格点Q(异于点C)的个数有8个,
故答案为:8;
(5)如图,点P即为所求.
点评 本题主要考查作图-平移变换,熟练掌握平移的定义和性质及三角形三边之间的关系是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知矩形的面积为1,设该矩形的长为x,周长为y,小彬借鉴以前研究函数的经验,对函数y随自变量x的变化进行了探究;以下是小彬的探究过程:
(1)结合问题情境分析:
①y与x的函数表达式为y=2x+$\frac{2}{x}$;②自变量x的取值范围是x>0.
(2)下表是y与x的几组对应值.
①写出m的值;
②画出函数图象;
③观察图象,写出该函数两条不同类型的性质.
(1)结合问题情境分析:
①y与x的函数表达式为y=2x+$\frac{2}{x}$;②自变量x的取值范围是x>0.
(2)下表是y与x的几组对应值.
| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{2}$ | $\frac{20}{3}$ | 5 | 4 | m | $\frac{20}{3}$ | $\frac{17}{2}$ | … |
②画出函数图象;
③观察图象,写出该函数两条不同类型的性质.
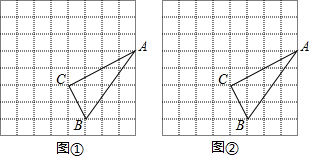 如图,小方格的边长为1,△ABC为格点三角形.
如图,小方格的边长为1,△ABC为格点三角形. 如图,把△ABC绕点A顺时针旋转20°至△ADE,且点B的对应点D在BC边上,则∠ADE的度数为80°.
如图,把△ABC绕点A顺时针旋转20°至△ADE,且点B的对应点D在BC边上,则∠ADE的度数为80°.