题目内容
4. 完成推理填空:
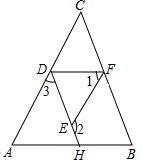
完成推理填空:如图在三角形ABC中,已知∠2+∠3=180°,∠1=∠A,试说明∠CFD=∠B.
解:∵∠2+∠DEF=180°(邻补角定义),∠2+∠3=180°(已知)
∴∠DEF=∠3(同角的补角相等)
∴AC∥EF(内错角相等,两直线平行)
∴∠CDF=∠1(两直线平行,内错角相等)
∵∠1=∠A(已知)
∴∠CDF=∠A(等量代换)
∴DF∥AB(同位角相等,两直线平行)
∴∠CFD=∠B(两直线平行.同位角相等)
分析 根据平行线的判定和性质即可得到结论.
解答 解:∵∠2+∠DEF=180°(邻补角定义),∠2+∠3=180°(已知)
∴∠DEF=∠3(同角的补角相等)
∴AC∥EF( 内错角相等,两直线平行)
∴∠CDF=∠1(两直线平行,内错角相等)
∵∠1=∠A(已知)
∴∠CDF=∠A(等量代换)
∴DF∥AB(同位角相等,两直线平行)
∴∠CFD=∠B.(两直线平行,同位角相等).
故答案为:∠DEF=∠3,内错角相等,两直线平行,∠1,同位角相等,两直线平行,两直线平行.同位角相等.
点评 此题主要考查了平行线的判定与性质,关键是掌握平行线的判定定理和性质定理.

练习册系列答案
相关题目
12.已知矩形的面积为1,设该矩形的长为x,周长为y,小彬借鉴以前研究函数的经验,对函数y随自变量x的变化进行了探究;以下是小彬的探究过程:
(1)结合问题情境分析:
①y与x的函数表达式为y=2x+$\frac{2}{x}$;②自变量x的取值范围是x>0.
(2)下表是y与x的几组对应值.
①写出m的值;
②画出函数图象;
③观察图象,写出该函数两条不同类型的性质.
(1)结合问题情境分析:
①y与x的函数表达式为y=2x+$\frac{2}{x}$;②自变量x的取值范围是x>0.
(2)下表是y与x的几组对应值.
| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{2}$ | $\frac{20}{3}$ | 5 | 4 | m | $\frac{20}{3}$ | $\frac{17}{2}$ | … |
②画出函数图象;
③观察图象,写出该函数两条不同类型的性质.
13.某经销商销售一批电子手表,第一个月以600元/块的价格售出60块,从第二个月起降价,以550元/块的价格将这批电子手表全部售出,销售总额超过了5.8万元.这批手表至少有( )
| A. | 100块 | B. | 101块 | C. | 103块 | D. | 105块 |
14.下列计算中,正确的是( )
| A. | (-3a2b)3=27a6b3 | B. | (a4)3=a7 | C. | a12÷a4=a8 | D. | a2•a4=a8 |
 如图,平面直角坐标系中,点A是直线y=$\frac{b}{a}x$(a≠0)上一点,过点A作AB⊥x轴于点B(2,0),若点C(4-a,b),且AC⊥OC,∠AOC=45°,OC与AB交于点D,求AD的长.
如图,平面直角坐标系中,点A是直线y=$\frac{b}{a}x$(a≠0)上一点,过点A作AB⊥x轴于点B(2,0),若点C(4-a,b),且AC⊥OC,∠AOC=45°,OC与AB交于点D,求AD的长.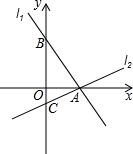 如图,过点A(2,0)的两条直线L1、L2分别交y轴于点B、C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.
如图,过点A(2,0)的两条直线L1、L2分别交y轴于点B、C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$. 如图,∵∠1=∠2(已知),∴AB∥CD,(内错角相等,两直线平行).
如图,∵∠1=∠2(已知),∴AB∥CD,(内错角相等,两直线平行).