题目内容
20.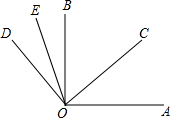 如图,已知∠AOB=90°,∠COE=70°,若OC平分∠AOB,OE平分∠DOB,求:
如图,已知∠AOB=90°,∠COE=70°,若OC平分∠AOB,OE平分∠DOB,求:(1)∠BOC和∠DOB的度数;
(2)将OA看作钟面上的时针,OB看作钟面上的分针,此时,钟面时间为3点,在3点到4点之间,经过多少分钟,OA、OB夹角为40°?
分析 (1)根据角平分线的定义和角的和差即可得到结论;
(2)分①当分针在时针上方时②当分针在时针下方时两种情况列出方程解答即可.
解答 解:(1)∵∠AOB=90°,∠COE=70°,若OC平分∠AOB,
∴∠BOC=45°,∠BOE=25°,
∵OE平分∠DOB,
∴∠BOD=2∠BOE=50°;
(2)设在下午3点至4点之间,从下午3点开始,经过x分钟,时针与分针成40° 角.
①当分针在时针上方时,
由题意得:(3+$\frac{x}{60}$)×30-6x=40,
解得:x=$\frac{100}{11}$
②当分针在时针下方时,
由题意得:6x-(3+$\frac{x}{60}$)×30=40
解得:x=$\frac{260}{11}$.
答:在下午3点至4点之间,从下午3点开始,经过$\frac{100}{11}$或$\frac{260}{11}$分钟,时针与分针成40° 角.
点评 本题考查的是角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.

练习册系列答案
相关题目
8.中国最美县城所在地推行全域旅游以来,乡村旅游十分红火,去年国庆黄金期间,美丽乡村民宿深受游客喜爱,某景区附近的A、B两家民宿在这一周内的日营业额日下表:
(1)要评价两家民宿日营业额的平均水平,你选择什么统计量?求出这个统计量.
(2)分别求出两家民宿两天营业额的方差,这两个方差的大小反映了什么?(结果精确到0.01)
| 日期(日) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| A店(千元) | 2 | 2.6 | 4.5 | 5 | 3.7 | 3.5 | 3.2 |
| B店(千元) | 2.9 | 2.9 | 3.7 | 4.8 | 4.2 | 3.1 | 2.9 |
(2)分别求出两家民宿两天营业额的方差,这两个方差的大小反映了什么?(结果精确到0.01)
5.一个不透明的盒子中装有3个红球,2个黄球和1个白球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是红球的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
12.已知矩形的面积为1,设该矩形的长为x,周长为y,小彬借鉴以前研究函数的经验,对函数y随自变量x的变化进行了探究;以下是小彬的探究过程:
(1)结合问题情境分析:
①y与x的函数表达式为y=2x+$\frac{2}{x}$;②自变量x的取值范围是x>0.
(2)下表是y与x的几组对应值.
①写出m的值;
②画出函数图象;
③观察图象,写出该函数两条不同类型的性质.
(1)结合问题情境分析:
①y与x的函数表达式为y=2x+$\frac{2}{x}$;②自变量x的取值范围是x>0.
(2)下表是y与x的几组对应值.
| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{2}$ | $\frac{20}{3}$ | 5 | 4 | m | $\frac{20}{3}$ | $\frac{17}{2}$ | … |
②画出函数图象;
③观察图象,写出该函数两条不同类型的性质.
13.某经销商销售一批电子手表,第一个月以600元/块的价格售出60块,从第二个月起降价,以550元/块的价格将这批电子手表全部售出,销售总额超过了5.8万元.这批手表至少有( )
| A. | 100块 | B. | 101块 | C. | 103块 | D. | 105块 |
 如图,直线a∥b,∠1=60°,∠2=40°,则∠3=80°.
如图,直线a∥b,∠1=60°,∠2=40°,则∠3=80°. 如图,平面直角坐标系中,点A是直线y=$\frac{b}{a}x$(a≠0)上一点,过点A作AB⊥x轴于点B(2,0),若点C(4-a,b),且AC⊥OC,∠AOC=45°,OC与AB交于点D,求AD的长.
如图,平面直角坐标系中,点A是直线y=$\frac{b}{a}x$(a≠0)上一点,过点A作AB⊥x轴于点B(2,0),若点C(4-a,b),且AC⊥OC,∠AOC=45°,OC与AB交于点D,求AD的长.