题目内容
17.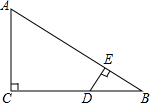 已知:如图,在△ABC中,∠C=90°,D是BC上一点,DE⊥AB于E,若AC=6,AB=10,DE=2.
已知:如图,在△ABC中,∠C=90°,D是BC上一点,DE⊥AB于E,若AC=6,AB=10,DE=2.(1)求证:△BED∽△BCA;
(2)求BD的长.
分析 (1)根据两角对应相等的两个三角形相似即可判定;
(2)利用相似三角形的性质即可解决问题;
解答 解:(1)∵DE⊥AB于E,
∴∠DEB=90°.
又∵∠C=90°,
∴∠DEB=∠C,
又∵∠B=∠B,
∴△BED∽△BCA.
(2)∵△BED∽△BCA,
∴$\frac{DE}{AC}$=$\frac{BD}{AB}$,
∴$\frac{2}{6}$=$\frac{BD}{10}$,
∴BD=$\frac{10}{3}$.
点评 本题考查相似三角形的判定和性质,解题的关键是熟练掌握相似三角形的判定方法,属于基础题,中考常考题型.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
8.中国最美县城所在地推行全域旅游以来,乡村旅游十分红火,去年国庆黄金期间,美丽乡村民宿深受游客喜爱,某景区附近的A、B两家民宿在这一周内的日营业额日下表:
(1)要评价两家民宿日营业额的平均水平,你选择什么统计量?求出这个统计量.
(2)分别求出两家民宿两天营业额的方差,这两个方差的大小反映了什么?(结果精确到0.01)
| 日期(日) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| A店(千元) | 2 | 2.6 | 4.5 | 5 | 3.7 | 3.5 | 3.2 |
| B店(千元) | 2.9 | 2.9 | 3.7 | 4.8 | 4.2 | 3.1 | 2.9 |
(2)分别求出两家民宿两天营业额的方差,这两个方差的大小反映了什么?(结果精确到0.01)
5.一个不透明的盒子中装有3个红球,2个黄球和1个白球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是红球的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
12.已知矩形的面积为1,设该矩形的长为x,周长为y,小彬借鉴以前研究函数的经验,对函数y随自变量x的变化进行了探究;以下是小彬的探究过程:
(1)结合问题情境分析:
①y与x的函数表达式为y=2x+$\frac{2}{x}$;②自变量x的取值范围是x>0.
(2)下表是y与x的几组对应值.
①写出m的值;
②画出函数图象;
③观察图象,写出该函数两条不同类型的性质.
(1)结合问题情境分析:
①y与x的函数表达式为y=2x+$\frac{2}{x}$;②自变量x的取值范围是x>0.
(2)下表是y与x的几组对应值.
| x | … | $\frac{1}{4}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | 4 | … |
| y | … | $\frac{17}{2}$ | $\frac{20}{3}$ | 5 | 4 | m | $\frac{20}{3}$ | $\frac{17}{2}$ | … |
②画出函数图象;
③观察图象,写出该函数两条不同类型的性质.
10.下列运算正确的是( )
| A. | $\sqrt{(-3)^{2}}$=3 | B. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ | D. | $\sqrt{5}$-$\sqrt{2}$=$\sqrt{3}$ |
 如图,平面直角坐标系中,点A是直线y=$\frac{b}{a}x$(a≠0)上一点,过点A作AB⊥x轴于点B(2,0),若点C(4-a,b),且AC⊥OC,∠AOC=45°,OC与AB交于点D,求AD的长.
如图,平面直角坐标系中,点A是直线y=$\frac{b}{a}x$(a≠0)上一点,过点A作AB⊥x轴于点B(2,0),若点C(4-a,b),且AC⊥OC,∠AOC=45°,OC与AB交于点D,求AD的长.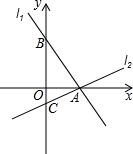 如图,过点A(2,0)的两条直线L1、L2分别交y轴于点B、C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.
如图,过点A(2,0)的两条直线L1、L2分别交y轴于点B、C,其中点B在原点上方,点C在原点下方,已知AB=$\sqrt{13}$.