题目内容
20.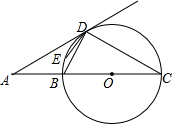 如图,BC是⊙O的直径,延长CB到点A使AB=$\frac{1}{2}$CB,过点A作射线AD,使AD与⊙O相切于点D,连接BD,CD.若点E是劣弧$\widehat{BD}$上一点,则∠BED的度数为150°.
如图,BC是⊙O的直径,延长CB到点A使AB=$\frac{1}{2}$CB,过点A作射线AD,使AD与⊙O相切于点D,连接BD,CD.若点E是劣弧$\widehat{BD}$上一点,则∠BED的度数为150°.
分析 连结OD,如图,由切线的性质得∠ADO=90°,再在Rt△AOD中利用三角函数的定义求出∠AOD=60°,然后根据三角形外角性质计算出∠C=30°,然后根据圆内接四边形的性质求∠BED的度数.
解答 解:连结OD,如图,
∵AD为切线,
∴OD⊥AD,
∴∠ADO=90°,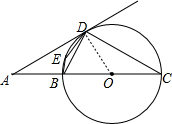
∵AB=$\frac{1}{2}$CB,BC是⊙O的直径
∴AB=OB=OA,
在Rt△AOD中,∵cos∠AOD=$\frac{OD}{OA}$=$\frac{1}{2}$,
∴∠AOD=60°,
∵OC=OD,
∴∠C=∠ODC,
而∠AOD=∠C+∠ODC,
∴∠C=$\frac{1}{2}∠$AOD=30°,
∵∠BED+∠C=180°,
∴∠BED=180°-30°=150°.
故答案为150°.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.解决本题的关键是求出∠AOD的度数.

练习册系列答案
相关题目
10.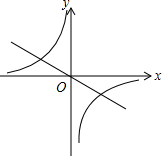 如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象都经过点A(2,-1),若y1>y2,则x的取值范围是( )
如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象都经过点A(2,-1),若y1>y2,则x的取值范围是( )
 如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象都经过点A(2,-1),若y1>y2,则x的取值范围是( )
如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象都经过点A(2,-1),若y1>y2,则x的取值范围是( )| A. | -1<x<0 | B. | x>2 | C. | -2<x<0或x>2 | D. | x<-2或0<x<2 |
5.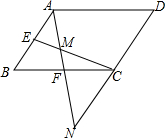 如图,在?ABCD中,E、F分别为AB、BC的中点,连接EC、AF,AF与EC交于点M,AF的延长线与DC的延长线交于点N.
如图,在?ABCD中,E、F分别为AB、BC的中点,连接EC、AF,AF与EC交于点M,AF的延长线与DC的延长线交于点N.
(1)求证:AB=CN;
(2)若△AEM的面积为2,求?ABCD的面积.
 如图,在?ABCD中,E、F分别为AB、BC的中点,连接EC、AF,AF与EC交于点M,AF的延长线与DC的延长线交于点N.
如图,在?ABCD中,E、F分别为AB、BC的中点,连接EC、AF,AF与EC交于点M,AF的延长线与DC的延长线交于点N.(1)求证:AB=CN;
(2)若△AEM的面积为2,求?ABCD的面积.
5. 如图所示的图案绕其中心旋转一定角度后能与自身重合,那么旋转的角度至少是( )
如图所示的图案绕其中心旋转一定角度后能与自身重合,那么旋转的角度至少是( )
 如图所示的图案绕其中心旋转一定角度后能与自身重合,那么旋转的角度至少是( )
如图所示的图案绕其中心旋转一定角度后能与自身重合,那么旋转的角度至少是( )| A. | 45° | B. | 60° | C. | 90° | D. | 180° |
6.若(x1,y1)(x2,y2)都是y=-$\frac{5}{x}$的图象上的点,且x1<x2<0,则下列各式正确的是( )
| A. | y1>y2>0 | B. | y1<y2<0 | C. | y2>y1>0 | D. | y2<0<y1 |
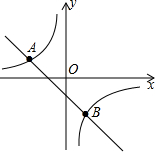 如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-2,1)、B(1,n)两点.若y1>y2,则x的取值范围是x<-2或0<x<1.
如图,一次函数y1=kx+b(k≠0)的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-2,1)、B(1,n)两点.若y1>y2,则x的取值范围是x<-2或0<x<1. 已知A(2,-2),B(-1,4)是一次函数y2=-2x+2的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB与y轴交于点C.
已知A(2,-2),B(-1,4)是一次函数y2=-2x+2的图象与反比例函数y=$\frac{m}{x}$的图象的两个交点,直线AB与y轴交于点C.