题目内容
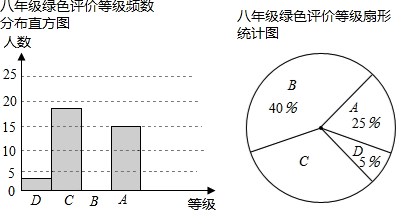
6.若(x1,y1)(x2,y2)都是y=-$\frac{5}{x}$的图象上的点,且x1<x2<0,则下列各式正确的是( )| A. | y1>y2>0 | B. | y1<y2<0 | C. | y2>y1>0 | D. | y2<0<y1 |
分析 先根据反比例函数的解析式判断出函数图象所在的象限,再根据x1<x2<0,判断出两点所在的象限,根据该函数在此象限内的增减性即可得出结论.
解答 解:∵反比例函数y=-$\frac{5}{x}$中,k=-5<0,
∴此函数图象的两个分支在二、四象限,
∵x1<x2<0,
∴两点在第二象限,
∵在第二象限内y的值随x的增大而增大,
∴0<y1<y2.
故选C.
点评 本题考查的是反比例函数图象上点的坐标特点,先根据题意判断出函数图象所在的象限及两点所在的象限是解答此题的关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
14.下列计算中,结果正确的是( )
| A. | a3•a2=a6 | B. | (a2)3=a6 | C. | (2a)(3a)=6a | D. | a6÷a2=a3 |
1.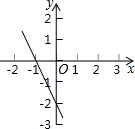 如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
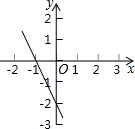 如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )| A. | x<-$\frac{1}{2}$ | B. | x>-$\frac{1}{2}$ | C. | x<-$\frac{1}{4}$ | D. | x>-$\frac{1}{4}$ |
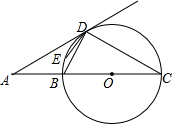 如图,BC是⊙O的直径,延长CB到点A使AB=$\frac{1}{2}$CB,过点A作射线AD,使AD与⊙O相切于点D,连接BD,CD.若点E是劣弧$\widehat{BD}$上一点,则∠BED的度数为150°.
如图,BC是⊙O的直径,延长CB到点A使AB=$\frac{1}{2}$CB,过点A作射线AD,使AD与⊙O相切于点D,连接BD,CD.若点E是劣弧$\widehat{BD}$上一点,则∠BED的度数为150°. 如图,A、B、C是一条公路边的三个连锁超市,且A、B、C在一条直线上,计划在A、C之间的公路边建一个配货中心P,负责向3个超市送货.
如图,A、B、C是一条公路边的三个连锁超市,且A、B、C在一条直线上,计划在A、C之间的公路边建一个配货中心P,负责向3个超市送货.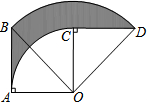 如图,在Rt△OAB中,∠AOB=45°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为π.
如图,在Rt△OAB中,∠AOB=45°,AB=2,将Rt△OAB绕O点顺时针旋转90°得到Rt△OCD,则AB扫过的面积为π.