题目内容
已知a＋b＝－4，ab＝2，求多项式4a2b＋4ab2－4a－4b的值。
－16
【解析】
试题分析：先根据分组分解法分解多项式4a2b＋4ab2－4a－4b，再整体代入求值即可得到结果.
当a＋b＝－4，ab＝2时，
4a2b＋4ab2－4a－4b＝4ab（a＋b）－4（a＋b）=4（a＋b）（ab－1）＝－16.
练习册系列答案
相关题目
如图，已知抛物线y＝
x2－
x－3与x轴的交点为A、D(A在D的右侧)，与y轴的交点为C.
(1)直接写出A、D、C三点的坐标；
(2)若点M在抛物线上，使得△MAD的面积与△CAD的面积相等，求点M的坐标；
(3)设点C关于抛物线对称轴的对称点为B，在抛物线上是否存在点P，使得以A、B、C、P四点为顶点的四边形为梯形？若存在，请求出点P的坐标；若不存在，请说明理由．
（1）A点坐标为(4，0)，D点坐标为(－2，0)，C点坐标为(0，－3)；
（2）M点坐标为(2，－3)或(1＋，3)或(1－，3)；
（3）在抛物线上存在一点P，使得以点A、B、C、P四点为顶点所构成的四边形为梯形；点P的坐标为(－2，0)或(6，6)．
【解析】试题分析：（1）在中令，解得，
∴A(4，0) 、D(－2，0).
在中令，得，∴C(0，－3).
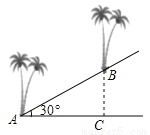
... 如图，在坡角为30°的斜坡上要栽两棵树，要求它们之间的水平距离AC为6m，则这两棵树之间的坡面AB的长为（ ）
A. 12m B. 3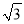
m C. 4
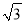m D. 12
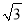m
C
【解析】试题分析：在Rt△ABC中，cos∠A=cos30°=，则AB=m，故选C． 抛物线y=x2－2x+3的顶点坐标是_______．
(1，2)
【解析】试题解析：∵y=x2-2x+3=x2-2x+1-1+3=（x-1）2+2，
∴抛物线y=x2-2x+3的顶点坐标是（1，2） 下列说法中错误的是( )
A ．在函数y＝－x2中，当x＝0时y有最大值0
B．在函数y＝2x2中，当x＞0时y随x的增大而增大
C．抛物线y＝2x2，y＝－x2，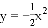
中，抛物线y＝2x2的开口最小，抛物线y＝－x2的开口最大
D．不论a是正数还是负数，抛物线y＝ax2的顶点都是坐标原点
C
【解析】由函数的解析式y＝－x2，可知a=-1＜0，得到函数的开口向下，有最大值y=0，故A正确；
由函数的解析式y＝2x2，可知其对称轴为y轴，对称轴的左边（x＜0），y随x增大而减小，对称轴的右边（x＞0），y随x增大而增大，故B正确；
根据二次函数的性质，可知系数a决定开口方向和开口大小，且a的值越大开口越小，可知抛物线y＝2x2的开口最小，抛物线y＝－x2的开口第二小... 如果x+y=5,xy=2,求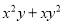
和
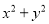的值
10；21.
【解析】试题分析：（1）因式分解后直接代入求值即可；（2）化为（x+y）2-2xy后代入求值即可.
试题解析：
∵x+y=5，xy=2，
∴=xy（x+y）=2×5=10；
=（x+y）2-2xy=52-2×2=25-4=21. 把（x－y）2－（y－x）分解因式为（ ）
A．（x－y）（x－y－1） B．（y－x）（x－y－1）
C．（y－x）（y－x－1） D．（y－x）（y－x＋1）
C
【解析】
试题分析：化（x－y）2－（y－x）=（y－x）2－（y－x），再提取公因式（y－x）即可得到结果.
（x－y）2－（y－x）=（y－x）2－（y－x）=（y－x）（y－x－1），故选C. 已知不论x为何值，x2-kx-15=(x+5)(x-3)，则k值为（ ）
A. 2 B. -2 C. 5 D. -3
B
【解析】∵x2-kx-15=(x+5)(x-3)=x2+2x-15，
∴k=-2.
故选B. 如果抛物线y=x2-6x+c-2的顶点到x轴的距离是3，那么c的值等于（ ）
A. 8
B. 14
C. 8或14
D. -8或-14
C
【解析】根据题意，得
，
解得c=8或14．
故选：C．