题目内容
把（x－y）2－（y－x）分解因式为（ ）
A．（x－y）（x－y－1） B．（y－x）（x－y－1）
C．（y－x）（y－x－1） D．（y－x）（y－x＋1）
C
【解析】
试题分析：化（x－y）2－（y－x）=（y－x）2－（y－x），再提取公因式（y－x）即可得到结果.
（x－y）2－（y－x）=（y－x）2－（y－x）=（y－x）（y－x－1），故选C.
练习册系列答案
相关题目
小汽车刹车距离s(m)与速度v(km/h)之间的函数关系式为s＝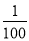
v2，一辆小汽车速度为100km/h，在前方80m处停放一辆故障车，此时刹车_______(填“会”或“不会”)有危险．
会
【解析】试题分析：由题意把代入即可求得s的值，与80比较即可判断.
在中，当时，
则此时刹车会有危险. 已知:如图，二次函数y=a（x﹣h）2+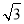
的图象经过原点O（0，0），A（2，0）．
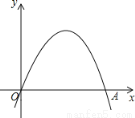
（1）写出该函数图象的对称轴；
（2）若将线段OA绕点O逆时针旋转60°到OA′，试判断点A′是否为该函数图象的顶点？请说明理由.
（1）直线x=1 （2）点A′为抛物线y=﹣（x﹣1）2+的顶点
【解析】
试题分析：（1）把已知点O、A代入函数的解析式可求出h的值h=1，及a=，然后根据二次函数的顶点式的特点判断出对称轴；
（2）由线段OA绕点O逆时针旋转60°到OA′，可知OA′=OA=2，∠A′OA=60°，如图，作A′B⊥x轴于点B，根据直角三角形的特点可知sin60°=，cos60°=,因此可求得A... 已知a＋b＝－4，ab＝2，求多项式4a2b＋4ab2－4a－4b的值。
－16
【解析】
试题分析：先根据分组分解法分解多项式4a2b＋4ab2－4a－4b，再整体代入求值即可得到结果.
当a＋b＝－4，ab＝2时，
4a2b＋4ab2－4a－4b＝4ab（a＋b）－4（a＋b）=4（a＋b）（ab－1）＝－16. 把多项式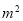
（a﹣2）+m（2﹣a）分解因式等于（ ）.
A．（a﹣2）（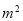
+m） B．（a﹣2）（
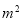﹣m）
C．m（a﹣2）（m﹣1） D．m（a﹣2）（m+1）
C．
【解析】
试题分析：先把（2﹣a）转化为（a﹣2），然后提取公因式m（a﹣2），可得（a﹣2）+m（2﹣a）= m（a﹣2）（m﹣1）.
故选：C． 在括号内填上适当的因式：(1) –x-1=-（______）;(2)a-b+c=a-（______）
x+1 b-c
【解析】根据添括号法则可得：(1) –x-1=-（x+1）；(2)a-b+c=a-（b-c）. 计算（1）～（3）题，并根据计算结果将（4）～（6）题进行分解因式.
（1）（x-2）（x-1）＝______； （2）3x（x-2）＝______；
（3）（x-2）2＝______； （4）3x2-6x＝______；
（5）x2-4x+4＝______； （6）x2-3x+2＝______.
x2-3x+2 3x2-6x x2-4x+4 3x(x-2) (x-2)2 (x-2)(x-1)
【解析】（1）根据多项式乘以多项式的乘法法则可得（x-2）（x-1）＝x2-3x+2；（2）根据单项式乘以多项式的乘法法则可得3x（x-2）＝3x2-6x；（3）根据完全平方公式可得（x-2）2＝x2-4x+4；（4）提取公因式3x可得3x2-6x＝3x(x-2)；（5）根据完全平方公式因式分解... 已知抛物线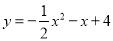
．
（1）用配方法求它的顶点坐标、对称轴；
（2）x取何值时，y随x增大而减小？
（3）x取何值时，抛物线在x轴上方？
（1）顶点坐标为（-1， ），对称轴为：x= -1；（2）x﹥-1时，随增大而减小 ；（3）-4﹤x﹤2时，抛物线在x轴上方．
【解析】试题分析：（1）用配方法时，先提二次项系数，再配方，写成顶点式，根据顶点式的坐标特点求顶点坐标及对称轴；
（2）对称轴是x=-1，开口向下，根据对称轴及开口方向确定函数的增减性；
（3）令y=0，确定函数图象与x轴的交点，结合开口方向判断x的取值... 已知抛物线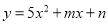
与x轴的交点为（
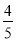，0）和（-2，0），则因式分解
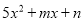的结果是__________
【解析】∵抛物线与x轴的交点为（，0）和（-2，0），a=5，
∴抛物线的解析式用交点式表示为
∴=
即： =．
故答案为： ．