题目内容
抛物线y=x2－2x+3的顶点坐标是_______．
(1，2)
【解析】试题解析：∵y=x2-2x+3=x2-2x+1-1+3=（x-1）2+2，
∴抛物线y=x2-2x+3的顶点坐标是（1，2）
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
直线y=3x-3与抛物线y=x2 －x+1的交点的个数是________ .
1
【解析】【解析】
假设直线y=3x﹣3与抛物线y=x2﹣x+1有交点，则3x﹣3=x2﹣x+1，x2﹣4x+4=0，∵△=16﹣16=0，∴方程有两个相等的实数根，∴直线y=3x﹣3与抛物线y=x2﹣x+1有1个交点．
故答案为：1． 如图，如果某个斜坡AB的长度为10米，且该斜坡最高点A到地面BC的铅垂高度为8米，求该斜坡的坡比
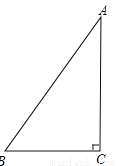
【解析】试题分析：首先根据AB和AC的长度以及勾股定理得出BC的长度，最后根据坡比的计算法则得出答案．
试题解析：∵某个斜坡AB的长度为10米，且该斜坡最高点A到地面BC的铅垂高度为8米，
∴水平距离BC= =6（m），
则该斜坡的坡比是： ． 如图，一个小球由地面沿着坡度i=1∶2的坡面向上前进了10 m，此时小球距离地面的高度为( )．
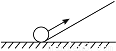
A．5m B．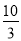
m C．4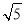
m D．2
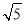m
D.
【解析】
试题分析：画出草图，根据题意用未知数表示相应的线段的长度，再运用勾股定理列方程求解即可．
试题解析：如图：
Rt△ABC中，tanA=，AB=10．
设BC=x，则AC=2x，
∴x2+（2x）2=102，
解得，（负值舍去）．
即此时小球距离地面的高度为米．
故选D. 已知:如图，二次函数y=a（x﹣h）2+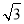
的图象经过原点O（0，0），A（2，0）．
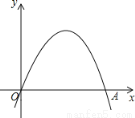
（1）写出该函数图象的对称轴；
（2）若将线段OA绕点O逆时针旋转60°到OA′，试判断点A′是否为该函数图象的顶点？请说明理由.
（1）直线x=1 （2）点A′为抛物线y=﹣（x﹣1）2+的顶点
【解析】
试题分析：（1）把已知点O、A代入函数的解析式可求出h的值h=1，及a=，然后根据二次函数的顶点式的特点判断出对称轴；
（2）由线段OA绕点O逆时针旋转60°到OA′，可知OA′=OA=2，∠A′OA=60°，如图，作A′B⊥x轴于点B，根据直角三角形的特点可知sin60°=，cos60°=,因此可求得A... 图中的圆点是有规律地从里到外逐层排列的．设y为第n层（n为正整数）圆点的个数，则下列函数关系中正确的是（ ）
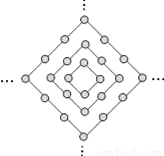
A. y=4n﹣4 B. y=4n C. y=4n+4 D. y=n2
B
【解析】试题解析：由题图可知：
n=1时，圆点有4个，即y=4；
n=2时，圆点有8个，即y=8；
n=3时，圆点有12个，即y=12；
……
∴y=4n.
故选：B. 已知a＋b＝－4，ab＝2，求多项式4a2b＋4ab2－4a－4b的值。
－16
【解析】
试题分析：先根据分组分解法分解多项式4a2b＋4ab2－4a－4b，再整体代入求值即可得到结果.
当a＋b＝－4，ab＝2时，
4a2b＋4ab2－4a－4b＝4ab（a＋b）－4（a＋b）=4（a＋b）（ab－1）＝－16. 在括号内填上适当的因式：(1) –x-1=-（______）;(2)a-b+c=a-（______）
x+1 b-c
【解析】根据添括号法则可得：(1) –x-1=-（x+1）；(2)a-b+c=a-（b-c）. 如图是二次函数y=ax2+bx+c的图象，下列结论： ①二次三项式ax2+bx+c的最大值为4；
②4a+2b+c＜0；
③一元二次方程ax2+bx+c=1的两根之和为﹣1；
④使y≤3成立的x的取值范围是x≥0．
其中正确的个数有（ ）
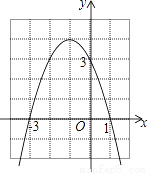
A. 1个 B. 2个 C. 3个 D. 4个
B
【解析】试题解析：∵抛物线的顶点坐标为（-1，4），∴二次三项式ax2+bx+c的最大值为4，①正确；
∵x=2时，y＜0，∴4a+2b+c＜0，②正确；
根据抛物线的对称性可知，一元二次方程ax2+bx+c=1的两根之和为-2，③错误；
使y≤3成立的x的取值范围是x≥0或x≤-2，④错误，
故选B．