题目内容
10．
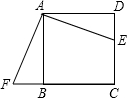如图，E是正方形ABCD的边DC上一点，过点A作FA=AE交CB的延长线于点F，若AB=4，则四边形AFCE的面积是（ ）| A． | 4 | B． | 8 | C． | 16 | D． | 无法计算 |
分析 由正方形ABCD中，FA=AE，易证得Rt△ABF≌Rt△ADE（HL），即可得S四边形AFCE=S正方形ABCD，求得答案．
解答 解：∵四边形ABCD是正方形，
∴∠ABC=∠D=90°，AB=AD，
即∠ABF=∠D=90°，
在Rt△ABF和Rt△ADE中，
$\left\{\begin{array}{l}{AB=AD}\\{AF=AE}\end{array}\right.$，
∴Rt△ABF≌Rt△ADE（HL），
∴SRt△ABF=SRt△ADE，
∴SRt△ABF+S四边形ABCE=SRt△ADE+S四边形ABCE，
∴S四边形AFCE=S正方形ABCD=16．
故选C．
点评 此题考查了正方形的性质以及全等三角形的判定与性质．注意证得Rt△ABF≌Rt△ADE是关键．
练习册系列答案
相关题目
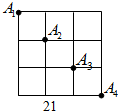如图，点A1、A2、A3、A4是某市正方形道路网的部分交汇点，且它们都位于同一对角线上．某人从点A1出发，规定向右或向下行走，那么到达点A3的走法共有6种．
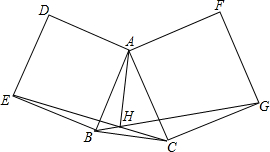在△ABC的边AB，AC向外作正方形ABED，ACGF，BG、CE相交于H．求证：AH⊥BC．
5．
如图，在正方形ABCD中，AB=8，Q是CD的中点，在CD上取一点P，使∠BAP=2∠DAQ，则CP的长度等于（ ）
如图，在正方形ABCD中，AB=8，Q是CD的中点，在CD上取一点P，使∠BAP=2∠DAQ，则CP的长度等于（ ）| A． | 1 | B． | 2 | C． | 3 | D． | $\sqrt{3}$ |
15．下面四省电视台标示图案中，属于轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
如图，点P是平行四边形ABCD对角线BD上的动点，点M为AD的中点，已知AD=8，AB=10，∠ABD=45°，把平行四边形ABCD绕着点A按逆时针方向旋转，点P的对应点是点Q，则线段MQ的长度的最大值与最小值的差为18-5$\sqrt{2}$．