题目内容

17．如图，四边形ABCD的两条对角线互相垂直，AC+BD=16，则四边形ABCD的面积最大值是（　　）
A．64B．16C．24D．32

分析 直接利用对角线互相垂直的四边形面积求法得出S=$\frac{1}{2}$AC•BD，再利用配方法求出二次函数最值．

解答 解：设AC=x，四边形ABCD面积为S，则BD=16-x，
则：S=$\frac{1}{2}$AC•BD=$\frac{1}{2}$x（16-x）=-$\frac{1}{2}$（x-8）2+32，
当x=8时，S最大=32；
所以AC=BD=8时，四边形ABCD的面积最大，
故选D．

点评 本题考查了二次函数最值以及四边形面积求法，正确掌握对角线互相垂直的四边形面积求法是解题关键．

练习册系列答案
相关题目
19．抛物线y=-3（x+$\frac{1}{2}$）2是由抛物线y=-3x2向左平移$\frac{1}{2}$个单位得到．
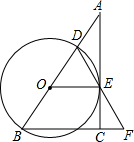8．如图，在Rt△ABC中，∠ACB=90°，点D是AB边上的一点，以BD为直径作⊙O，过O作AC的垂线交AC于点E，恰好垂足E在⊙O上，连接DE并延长DE交BC的延长线于点F．
（1）求证：BD=BF；
（2）若CF=2，cosB=$\frac{3}{5}$，求⊙O的半径．
5．如图，在正方形ABCD中，AB=8，Q是CD的中点，在CD上取一点P，使∠BAP=2∠DAQ，则CP的长度等于（　　）
A．1B．2C．3D．$\sqrt{3}$
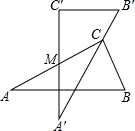12．两块完全一样的含30°角的直角三角板，将它们重叠在一起并绕其较长直角边的中点M转动，使上面一块三角板的斜边刚好过下面一块三角板的直角顶点C，如图所示．已知AC=6，则这两块直角三角板顶点A、A′之间的距离等于3．
2．动手操作：小明利用等距平行线解决了二等分线段的问题．
作法：
（1）在e上任取一点C，以点C为圆心，AB长为半径画弧交c于点D，交d于点E；
（2）以点A为圆心，CE长为半径画弧交AB于点M；∴点M为线段AB的二等分点．

解决下列问题：（尺规作图，保留作图痕迹）
（1）仿照小明的作法，在图2中作出线段AB的三等分点；
（2）点P是∠AOB内部一点，过点P作PM⊥OA于M，PN⊥OB于N，请找出一个满足下列条件的点P．（可以利用图1中的等距平行线）
①在图3中作出点P，使得PM=PN；
②在图4中作出点P，使得PM=2PN．
9．如图1，矩形OABC在平面直角坐标系中，O为坐标原点，点A（0，4），C（2，0），将矩形OABC绕点O按顺时针旋转30°，得到矩形EFGH（点E与O重合）．
（1）求点F的坐标，并判断点F是否在线段BC上；
（2）如图2，将矩形FEGH沿y轴向下平移m个单位，
①当四边形OFCE是平行四边形使，则m的值是多少？此时过点O作直线l将?OFCE分为面积比为1：3的两部分，求直线l的解析式；
②设矩形EFGH沿y轴向下平移过程中与矩形OABC重叠部分面积为S，写出S关于m的解析式，并求当S：S矩形ABCO=$\sqrt{3}$：6时m的值．
6．如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a≠0）与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，点A的坐标为（-1，0），且OC=OB，tan∠ACO=$\frac{1}{4}$．
（1）求抛物线的解析式；
（2）若点D和点C关于抛物线的对称轴对称，直线AD下方的抛物线上有一点P，过点P作PH⊥AD于点H，作PM平行于y轴交直线AD于点M，交x轴于点E，求△PHM的周长的最大值；
（3）在（2）的条件下，以点E为端点，在直线EP的右侧作一条射线与抛物线交于点N，使得∠NEP为锐角，在线段EB上是否存在点G，使得以E，N，G为顶点的三角形与△AOC相似？如果存在，请求出点G的坐标；如果不存在，请说明理由．
7．在直角三角形ABC中，BC=6cm，AC=8cm，点D在线段AC上从C向A运动．若设CD=x（m），△ABD的面积为因变量y．
（1）请写出y与x的关系式；
（2）当x为何值时，y有最大值，最大值是多少？此时点D在什么位置？
（3）当△ABD的面积是△ABC的面积的四分之一时，点D在什么位置？
（4）若有两个动点同时从C点出发，一个沿着CA方向，以1.5cm/秒到达F点，另一个沿着CB方向，以2cm/秒到达E点（E点可能在CB的延长线上）．请问构成的△ECF有没有可能与△ACB全等？如果有可能，请你说明理由；如果不可能，也请说明原因．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网