题目内容
7.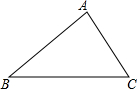 小明家有一块三角形的土地,如图所示,其三边长AB=70米,BC=90米,AC=50米,现要把△ABC分成面积比为5:7:9的三部分,分别种植不同的农作物,请你设计一种方案.
小明家有一块三角形的土地,如图所示,其三边长AB=70米,BC=90米,AC=50米,现要把△ABC分成面积比为5:7:9的三部分,分别种植不同的农作物,请你设计一种方案.
分析 如图作△ABC的角平分线,交点为O,则S△AOC:S△ABO:S△BOC=5:7:9.
解答  解:如图作△ABC的角平分线,交点为O,则S△AOC:S△ABO:S△BOC=5:7:9理由如下,
解:如图作△ABC的角平分线,交点为O,则S△AOC:S△ABO:S△BOC=5:7:9理由如下,
作OE⊥AB,OF⊥BC,OG⊥AC垂足分别为E、F、G.
∵点O是△ABC的角平分线的交点,AC=50,AB=70,BC=90,
∴OE=0F=OG,
∴S△AOC:S△ABO:S△BOC=$\frac{1}{2}$•AC•OG:$\frac{1}{2}$•AB•OE:$\frac{1}{2}$•BC•OF=AC:AB:BC=5:7:9.
点评 本题考查作图设计、角平分线的性质、三角形的面积等知识,正确利用角平分线的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.用“★”规定新运算:对于任意实数a,b,都有a★b=a2-b,如果x★13=2,那么x等于( )
| A. | 15 | B. | $\sqrt{15}$ | C. | $-\sqrt{15}$ | D. | ±$\sqrt{15}$ |
5. 如图,在正方形ABCD中,AB=8,Q是CD的中点,在CD上取一点P,使∠BAP=2∠DAQ,则CP的长度等于( )
如图,在正方形ABCD中,AB=8,Q是CD的中点,在CD上取一点P,使∠BAP=2∠DAQ,则CP的长度等于( )
 如图,在正方形ABCD中,AB=8,Q是CD的中点,在CD上取一点P,使∠BAP=2∠DAQ,则CP的长度等于( )
如图,在正方形ABCD中,AB=8,Q是CD的中点,在CD上取一点P,使∠BAP=2∠DAQ,则CP的长度等于( )| A. | 1 | B. | 2 | C. | 3 | D. | $\sqrt{3}$ |
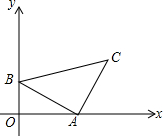 如图,在△ABC中,∠C=45°,∠BAC=90°,点A为($\sqrt{3}$,0)、点B为(0,1),坐标系内有一动点P,使得以P、A、C为顶点的三角形和△ABC全等,则P点坐标为(1,$\sqrt{3}$+1)、(2$\sqrt{3}$,-1)、(2$\sqrt{3}$+1,$\sqrt{3}$-1).
如图,在△ABC中,∠C=45°,∠BAC=90°,点A为($\sqrt{3}$,0)、点B为(0,1),坐标系内有一动点P,使得以P、A、C为顶点的三角形和△ABC全等,则P点坐标为(1,$\sqrt{3}$+1)、(2$\sqrt{3}$,-1)、(2$\sqrt{3}$+1,$\sqrt{3}$-1).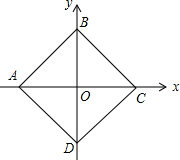 如图,在平面直角坐标系中,四边形ABCD是正方形,AB=$\sqrt{2}$,则点A的坐标为(-1,0)、点B的坐标为(0,1)、点C的坐标为(1,0)、点D的坐标为(0,-1).
如图,在平面直角坐标系中,四边形ABCD是正方形,AB=$\sqrt{2}$,则点A的坐标为(-1,0)、点B的坐标为(0,1)、点C的坐标为(1,0)、点D的坐标为(0,-1).