题目内容
16．
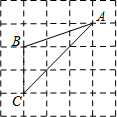如图，△ABC的三个顶点均在格点上，则cosA的值为（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{5}}{5}$ | C． | 2 | D． | $\frac{2\sqrt{5}}{5}$ |
分析 过B点作BD⊥AC，得AB的长，AD的长，利用锐角三角函数得结果．
解答 解：过B点作BD⊥AC，如图，
由勾股定理得，
AB=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$，
AD=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$，
cosA=$\frac{AD}{AB}$=$\frac{2\sqrt{2}}{\sqrt{10}}$=$\frac{2\sqrt{5}}{5}$，
故选D．
点评 本题考查了锐角三角函数和勾股定理，作出适当的辅助线构建直角三角形是解答此题的关键．
练习册系列答案
相关题目
6．下列运算正确的是（ ）
| A． | （ab）3=a3b | B． | （a+b）2=a2+b2 | C． | a6÷a2=a3 | D． | π0=1 |
如图，AB∥DE，△ACB是等腰直角三角形，且∠C=90°，CB的延长线交DE于点G，则∠CGE=135度．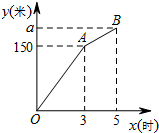
甲、乙两个工程队同时开始维修某一段路面，一段时间后，甲队被调往别处，乙队又用了2小时完成了剩余的维修任务．已知乙队每小时维修路面的长度保持不变，甲队每小时维修路面30米．甲、乙两队在此路段维修路面的总长度y（米）与维修时间x（时）之间的函数图象如图所示．
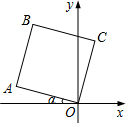将边长为2的正方形OABC如图放置，O为原点．若∠α=15°，则点B的坐标为（-$\sqrt{2}$，$\sqrt{6}$）．
8．下列运算正确的是（ ）
| A． | a2+a3=a5 | B． | 4a+2b=6ab | C． | ${（\frac{1}{{{a^2}+1}}）^0}=1$ | D． | ${（2\sqrt{5}）^2}=10$ |