题目内容
17．先化简，再求值：$\frac{1}{x+1}$-$\frac{x+3}{{x}^{2}-1}$÷$\frac{{x}^{2}+4x+3}{{x}^{2}+2x+1}$，已知x=$\sqrt{3}$．分析 先把原式根据分式的除法法则和异分母分式加减法法则化简，再把已知数据代入计算即可．
解答 解：原式=$\frac{1}{x+1}$-$\frac{x+3}{（x+1）（x-1）}$×$\frac{（{x+1）}^{2}}{（x+1）（x+3）}$
=$\frac{1}{x+1}$-$\frac{1}{x-1}$
=$\frac{2}{1-{x}^{2}}$，
当x=$\sqrt{3}$时，原式=$\frac{2}{1-（\sqrt{3}）^{2}}$=-1．
点评 本题考查的是分式的化简求值，在化简的过程中要注意运算顺序和分式的化简．化简的最后结果分子、分母要进行约分，注意运算的结果要化成最简分式或整式．
练习册系列答案
相关题目
如图，AB∥DE，△ACB是等腰直角三角形，且∠C=90°，CB的延长线交DE于点G，则∠CGE=135度．
8．下列运算正确的是（ ）
| A． | a2+a3=a5 | B． | 4a+2b=6ab | C． | ${（\frac{1}{{{a^2}+1}}）^0}=1$ | D． | ${（2\sqrt{5}）^2}=10$ |
2．
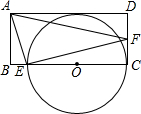如图，矩形ABCD中，E为BC上一点，F为CD上一点，∠AEF=90°，以EC为直径的⊙O与AD相切，则tan∠AFE的值为（ ）
如图，矩形ABCD中，E为BC上一点，F为CD上一点，∠AEF=90°，以EC为直径的⊙O与AD相切，则tan∠AFE的值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{4}$ |
