题目内容
1.解方程组$\left\{\begin{array}{l}{x+2y+3z=1}\\{2x+3y+z=2}\\{3x+y+2z=3}\end{array}\right.$.分析 先将三元一次方程组通过加减消元法转化为二元一次方程组,再通过加减消元法转化为一元一次方程,从而可以解答本题.
解答 解:$\left\{\begin{array}{l}{x+2y+3z=1}&{①}\\{2x+3y+z=2}&{②}\\{3x+y+2z=3}&{③}\end{array}\right.$,
①×2-②,得y+5z=0④,
①×3-③,得5y+7z=0⑤,
④×5-⑤,得13z=0,
解得z=0,
将z=0代入⑤,得y=0,
将y=0,z=0代入①得x=1.
故原方程组的解是$\left\{\begin{array}{l}{x=1}\\{y=0}\\{z=0}\end{array}\right.$.
点评 本题考查解三元一次方程组,解题的关键是利用加减消元法将方程组转化为一元一次方程进行解答.

练习册系列答案
相关题目
16.若点P的坐标是(x,y),且满足x2+$\sqrt{y}$=0,则点P在( )
| A. | x轴的负半轴上 | B. | 第二象限 | C. | y轴的正半轴上 | D. | 坐标原点 |
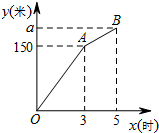 甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队又用了2小时完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度y(米)与维修时间x(时)之间的函数图象如图所示.
甲、乙两个工程队同时开始维修某一段路面,一段时间后,甲队被调往别处,乙队又用了2小时完成了剩余的维修任务.已知乙队每小时维修路面的长度保持不变,甲队每小时维修路面30米.甲、乙两队在此路段维修路面的总长度y(米)与维修时间x(时)之间的函数图象如图所示.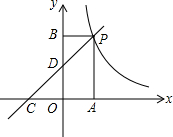 如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,S△PBD=2,OA=OC.求:
如图,一次函数y=kx+2的图象与反比例函数y=$\frac{m}{x}$的图象交于点P,点P在第一象限,PA⊥x轴于点A,PB⊥y轴于点B,一次函数的图象分别交x轴、y轴于点C、D,S△PBD=2,OA=OC.求: