题目内容
16.在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以C为圆心,5为半径的圆上,连结PA,PB.若PB=4,则PA的长为3或$\sqrt{73}$.分析 连结CP,PB的延长线交⊙C于P′,如图,先计算出CB2+PB2=CP2,则根据勾股定理的逆定理得∠CBP=90°,再根据垂径定理得到PB=P′B=4,接着证明四边形ACBP为矩形,则PA=BC=3,然后在Rt△APP′中利用勾股定理计算出P′A=$\sqrt{73}$,从而得到满足条件的PA的长为3或$\sqrt{73}$.
解答 解: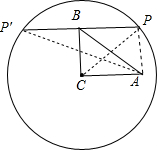 连结CP,PB的延长线交⊙C于P′,如图,
连结CP,PB的延长线交⊙C于P′,如图,
∵CP=5,CB=3,PB=4,
∴CB2+PB2=CP2,
∴△CPB为直角三角形,∠CBP=90°,
∴CB⊥PB,
∴PB=P′B=4,
∵∠C=90°,
∴PB∥AC,
而PB=AC=4,
∴四边形ACBP为矩形,
∴PA=BC=3,
在Rt△APP′中,∵PA=3,PP′=8,
∴P′A=$\sqrt{{8}^{2}+{3}^{2}}$=$\sqrt{73}$,
∴PA的长为3或$\sqrt{73}$.
故答案为3或$\sqrt{73}$.
点评 本题考查了点与圆的位置关系:点的位置可以确定该点到圆心距离与半径的关系,反过来已知点到圆心距离与半径的关系可以确定该点与圆的位置关系.也考查了垂径定理和勾股定理.

练习册系列答案
相关题目
6. 如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,且BD=3AD.那么AE:AC等于( )
如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,且BD=3AD.那么AE:AC等于( )
 如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,且BD=3AD.那么AE:AC等于( )
如图,已知D,E分别是△ABC的AB,AC边上的点,DE∥BC,且BD=3AD.那么AE:AC等于( )| A. | 2:3 | B. | 1:2 | C. | 1:3 | D. | 1:4 |
7.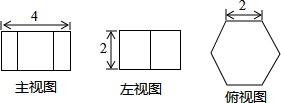 如图是某几何体的三视图,则该几何体的表面积为( )
如图是某几何体的三视图,则该几何体的表面积为( )
 如图是某几何体的三视图,则该几何体的表面积为( )
如图是某几何体的三视图,则该几何体的表面积为( )| A. | 16+6$\sqrt{3}$ | B. | 16+12$\sqrt{3}$ | C. | 24+6$\sqrt{3}$ | D. | 24+12$\sqrt{3}$ |
8.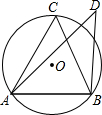 如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )
如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )
 如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )
如图,若锐角△ABC内接于⊙O,点D在⊙O外(与点C在AB同侧),则下列三个结论:①sin∠C>sin∠D;②cos∠C>cos∠D;③tan∠C>tan∠D中,正确的结论为( )| A. | ①② | B. | ②③ | C. | ①②③ | D. | ①③ |
5.下列几何体的主视图与其他三个不同的是( )
| A. |  | B. |  | C. |  | D. |  |
6.甲、乙两布袋装有红、白两种小球,两袋装球总数量相同,两种小球仅颜色不同.甲袋中,红球个数是白球个数的2倍;乙袋中,红球个数是白球个数的3倍,将乙袋中的球全部倒入甲袋,随机从甲袋中摸出一个球,摸出红球的概率是( )
| A. | $\frac{5}{12}$ | B. | $\frac{7}{12}$ | C. | $\frac{17}{24}$ | D. | $\frac{2}{5}$ |
 酒驾猛于虎,但很多人不以为是,为了加强人们对酒驾危害的认识,交警部门加大了对酒驾的检查力度.某市交警在2015年2月28日这天对本市各大主要交通路口进行车辆检查,如图,AC是该市解放路的一段,AE,BF,CD都是南北方向的街道,与解放路AC的交叉路口分别是A,B,C.已知出警点D位于点A的北偏东45°方向、点B的北偏东30°方向上,BD=2km,∠DBC=30°.
酒驾猛于虎,但很多人不以为是,为了加强人们对酒驾危害的认识,交警部门加大了对酒驾的检查力度.某市交警在2015年2月28日这天对本市各大主要交通路口进行车辆检查,如图,AC是该市解放路的一段,AE,BF,CD都是南北方向的街道,与解放路AC的交叉路口分别是A,B,C.已知出警点D位于点A的北偏东45°方向、点B的北偏东30°方向上,BD=2km,∠DBC=30°.