题目内容
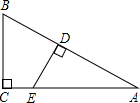 如图,Rt△ABC中,∠C=90°,∠A=30°,点D、E分别在AB、AC上,且DE⊥AB,若DE将△ABC分成面积相等的两部分,那么线段CE与AE的长度的比是
如图,Rt△ABC中,∠C=90°,∠A=30°,点D、E分别在AB、AC上,且DE⊥AB,若DE将△ABC分成面积相等的两部分,那么线段CE与AE的长度的比是考点:相似三角形的判定与性质,勾股定理
专题:计算题
分析:根据Rt△ABC中,∠C=90°和DE⊥AB,证明△ABC∽△AED,然后利用相似三角形面积比等于相似比的平方,即可解题.
解答:解;由Rt△ABC中,∠C=90°和DE⊥AB得△ABC∽△AED,
即
=
,
∴
=
设AE=x,AD=
x,
又∵
=
,
∴AC=
x,
CE=
x-x,
=
=
.
故答案为:
.
即
| s△ABC |
| s△AED |
| AC2 |
| AE2 |
∴
| AD |
| AC |
| ||
| 1 |
设AE=x,AD=
| ||
| 2 |
又∵
| AD |
| AC |
| ||
| 1 |
∴AC=
| ||
| 2 |
CE=
| ||
| 2 |
| CE |
| AE |
| ||||
| 1 |
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:此题主要考查学生对相似三角形的判定与性质和勾股定理的理解和掌握.

练习册系列答案
相关题目
 如图,等腰梯形ABCD中,上底AD=5cm,下底BC=8cm,以CD为边向外作正方形CDEF,则△EAD的面积等于
如图,等腰梯形ABCD中,上底AD=5cm,下底BC=8cm,以CD为边向外作正方形CDEF,则△EAD的面积等于 如图,正方形ABCD内有一个内接△AEF,若∠EAF=45°,AB=8厘米,EF=7厘米,则△EFC的面积是
如图,正方形ABCD内有一个内接△AEF,若∠EAF=45°,AB=8厘米,EF=7厘米,则△EFC的面积是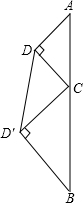 如图,直线段AB的长为l,C为AB上的一个动点,分别以AC和BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCD′,那么DD′的长的最小值为
如图,直线段AB的长为l,C为AB上的一个动点,分别以AC和BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCD′,那么DD′的长的最小值为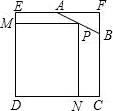 如图,已知边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=1.在AB上的一点P,使得矩形PNDM有最大面积,则矩形PNDM面积的最大值是( )
如图,已知边长为4的正方形截去一角成为五边形ABCDE,其中AF=2,BF=1.在AB上的一点P,使得矩形PNDM有最大面积,则矩形PNDM面积的最大值是( )