题目内容
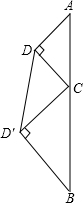 如图,直线段AB的长为l,C为AB上的一个动点,分别以AC和BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCD′,那么DD′的长的最小值为
如图,直线段AB的长为l,C为AB上的一个动点,分别以AC和BC为斜边在AB的同侧作两个等腰直角三角形△ACD和△BCD′,那么DD′的长的最小值为考点:二次函数的最值,勾股定理,等腰直角三角形
专题:计算题
分析:设AC=x,BC=l-x,∵△ABC,△BCD′均为等腰直角三角形,∴CD=
x,CD′=
(l-x),∵∠ACD=45°,∠BCD′=45°,∴∠DCD′=90°,根据勾股定理然后用配方法即可求解.
| ||
| 2 |
| ||
| 2 |
解答:解:设AC=x,BC=l-x,
∵△ABC,△BCD′均为等腰直角三角形,
∴CD=
x,CD′=
(l-x),
∵∠ACD=45°,∠BCD′=45°,
∴∠DCD′=90°,
∴DD′2=CD2+CD′2=
x2+
(l-x)2
=x2-lx+
l2=(x-
l)2+
l2,
∴当x取
l时,DD′取最小值,最小值为:
l.
故答案为:
l.
∵△ABC,△BCD′均为等腰直角三角形,
∴CD=
| ||
| 2 |
| ||
| 2 |
∵∠ACD=45°,∠BCD′=45°,
∴∠DCD′=90°,
∴DD′2=CD2+CD′2=
| 1 |
| 2 |
| 1 |
| 2 |
=x2-lx+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴当x取
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查了二次函数最值及等腰直角三角形,难度不大,关键是掌握用配方法求二次函数最值.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
 下面所说的“平移”,是指只沿方格的格线(即上下或左右)运动,将图中的任一条线段平移1格称为“1步”.要通过平移,使图中的3条线段首尾相接组成一个三角形,最少需要移动( )
下面所说的“平移”,是指只沿方格的格线(即上下或左右)运动,将图中的任一条线段平移1格称为“1步”.要通过平移,使图中的3条线段首尾相接组成一个三角形,最少需要移动( )| A、7步 | B、8步 | C、9步 | D、10步 |
 如图,△ABC的边AB=30cm,AC=25cm,点D、F在AC上,点E、G在AB上,S△ADE:S△DEF:S△EFG:S△FGC:S△GBC=1:2:3:4:5(S△XYZ表示△XYZ的面积).求AD和EG的长.
如图,△ABC的边AB=30cm,AC=25cm,点D、F在AC上,点E、G在AB上,S△ADE:S△DEF:S△EFG:S△FGC:S△GBC=1:2:3:4:5(S△XYZ表示△XYZ的面积).求AD和EG的长.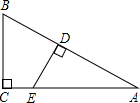 如图,Rt△ABC中,∠C=90°,∠A=30°,点D、E分别在AB、AC上,且DE⊥AB,若DE将△ABC分成面积相等的两部分,那么线段CE与AE的长度的比是
如图,Rt△ABC中,∠C=90°,∠A=30°,点D、E分别在AB、AC上,且DE⊥AB,若DE将△ABC分成面积相等的两部分,那么线段CE与AE的长度的比是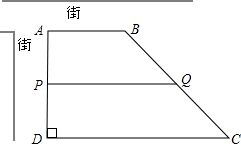 如图,现有一块梯形土地ABCD要出售,已测得上底AB=200m,高AD=230m,∠D=90°,∠C=45°.康宁房地产公司计划购买两面沿街的一块面积为25000m2的梯形地块ABQP,试求AP的长.
如图,现有一块梯形土地ABCD要出售,已测得上底AB=200m,高AD=230m,∠D=90°,∠C=45°.康宁房地产公司计划购买两面沿街的一块面积为25000m2的梯形地块ABQP,试求AP的长.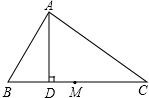 如图,在△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点,AB=10厘米,则MD的长为
如图,在△ABC中,∠B=2∠C,AD⊥BC于D,M为BC的中点,AB=10厘米,则MD的长为 如图,平行四边形ABCD中,∠A是它的外角的
如图,平行四边形ABCD中,∠A是它的外角的