题目内容
 如图,等腰梯形ABCD中,上底AD=5cm,下底BC=8cm,以CD为边向外作正方形CDEF,则△EAD的面积等于
如图,等腰梯形ABCD中,上底AD=5cm,下底BC=8cm,以CD为边向外作正方形CDEF,则△EAD的面积等于考点:等腰梯形的性质,正方形的性质
专题:计算题
分析:先做AD延长线上的辅助线:EG⊥AD的延长线于G,CH⊥AD的延长线于H,由此可EG的长度,即可得三角形AED的面积.
解答:解:作EG⊥AD的延长线于G,CH⊥AD的延长线于H.
如图所示:∵∠EDG=∠DCH(均为∠CDH的余角);
∠EGD=∠DHC=90°,
已知DE=CD,
∴△DGE≌△CHD(ASA).
则EG=DH=(BC-AD)/2=3/2.
所以:S△EAD=AD•
=5•
•
=
cm2.
故答案为:
.
如图所示:∵∠EDG=∠DCH(均为∠CDH的余角);

∠EGD=∠DHC=90°,
已知DE=CD,
∴△DGE≌△CHD(ASA).
则EG=DH=(BC-AD)/2=3/2.
所以:S△EAD=AD•
| EG |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 15 |
| 4 |
故答案为:
| 15 |
| 4 |
点评:本题考查了等腰梯形的性质和正方形的性质,难度较大,做题的关键在于画出辅助线,证明△DGE≌△CHD.

练习册系列答案
相关题目
 如图,一张长方形桌子可坐6人.那么将两张这样的桌子拼成一张大桌子后,最多可坐
如图,一张长方形桌子可坐6人.那么将两张这样的桌子拼成一张大桌子后,最多可坐 如图,△ABC的边AB=30cm,AC=25cm,点D、F在AC上,点E、G在AB上,S△ADE:S△DEF:S△EFG:S△FGC:S△GBC=1:2:3:4:5(S△XYZ表示△XYZ的面积).求AD和EG的长.
如图,△ABC的边AB=30cm,AC=25cm,点D、F在AC上,点E、G在AB上,S△ADE:S△DEF:S△EFG:S△FGC:S△GBC=1:2:3:4:5(S△XYZ表示△XYZ的面积).求AD和EG的长.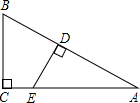 如图,Rt△ABC中,∠C=90°,∠A=30°,点D、E分别在AB、AC上,且DE⊥AB,若DE将△ABC分成面积相等的两部分,那么线段CE与AE的长度的比是
如图,Rt△ABC中,∠C=90°,∠A=30°,点D、E分别在AB、AC上,且DE⊥AB,若DE将△ABC分成面积相等的两部分,那么线段CE与AE的长度的比是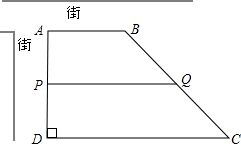 如图,现有一块梯形土地ABCD要出售,已测得上底AB=200m,高AD=230m,∠D=90°,∠C=45°.康宁房地产公司计划购买两面沿街的一块面积为25000m2的梯形地块ABQP,试求AP的长.
如图,现有一块梯形土地ABCD要出售,已测得上底AB=200m,高AD=230m,∠D=90°,∠C=45°.康宁房地产公司计划购买两面沿街的一块面积为25000m2的梯形地块ABQP,试求AP的长. 如图,矩形ABCD中,E,F分别是BC,CD上的点,且S△ABE=2,S△CEF=3,S△ADF=4,则S△AEF=
如图,矩形ABCD中,E,F分别是BC,CD上的点,且S△ABE=2,S△CEF=3,S△ADF=4,则S△AEF=