题目内容
 如图,正方形ABCD内有一个内接△AEF,若∠EAF=45°,AB=8厘米,EF=7厘米,则△EFC的面积是
如图,正方形ABCD内有一个内接△AEF,若∠EAF=45°,AB=8厘米,EF=7厘米,则△EFC的面积是考点:旋转的性质,全等三角形的判定与性质
专题:计算题
分析:延长EB到G,使BG=DF,连接AG,易得△ABG≌△ADF,所以∠GAB=∠FAD,而∠BAE+∠FAD=45°,得到∠GBA+∠BAE=45°,可证得∴△AEF≌△AEG,因此S△EFC=S正方形ABCD-2S△AEG,分别计算正方形和三角形的面积即可.
解答: 解:延长EB到G,使BG=DF,连接AG,如图,
解:延长EB到G,使BG=DF,连接AG,如图,
∵AB=AD,
∴△ABG≌△ADF,
∴∠GAB=∠FAD,
∵∠EAF=45°,
∴∠BAE+∠FAD=45°,
∴∠GBA+∠BAE=45°,
在△AEF和△AEG中,AE=AE,AF=AG,∠EAF=∠EAG=45°,
∴△AEF≌△AEG,
∴EF=EG=7,
∴S△EFC=S正方形ABCD-2S△AEG=8×8-2×
×7×8=8(cm2).
故答案为:8cm2.
 解:延长EB到G,使BG=DF,连接AG,如图,
解:延长EB到G,使BG=DF,连接AG,如图,∵AB=AD,
∴△ABG≌△ADF,
∴∠GAB=∠FAD,
∵∠EAF=45°,
∴∠BAE+∠FAD=45°,
∴∠GBA+∠BAE=45°,
在△AEF和△AEG中,AE=AE,AF=AG,∠EAF=∠EAG=45°,
∴△AEF≌△AEG,
∴EF=EG=7,
∴S△EFC=S正方形ABCD-2S△AEG=8×8-2×
| 1 |
| 2 |
故答案为:8cm2.
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了正方形的性质.

练习册系列答案
相关题目
求值:20063-10063-10003-3000×2006×1006=( )
| A、2036216432 |
| B、2000000000 |
| C、12108216000 |
| D、0 |
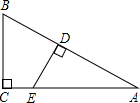 如图,Rt△ABC中,∠C=90°,∠A=30°,点D、E分别在AB、AC上,且DE⊥AB,若DE将△ABC分成面积相等的两部分,那么线段CE与AE的长度的比是
如图,Rt△ABC中,∠C=90°,∠A=30°,点D、E分别在AB、AC上,且DE⊥AB,若DE将△ABC分成面积相等的两部分,那么线段CE与AE的长度的比是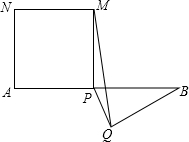 如图,P为经段AB上一点,以AP为边作一正方形APMN,以BP为底在另一侧作等腰△BPQ,连接MQ,若AB的长为4,则△MPQ的面积的最大值等于
如图,P为经段AB上一点,以AP为边作一正方形APMN,以BP为底在另一侧作等腰△BPQ,连接MQ,若AB的长为4,则△MPQ的面积的最大值等于