题目内容
设M是边长为2的正三角形ABC的边AB上的中点,P是边长BC上的任意一点,求PA+PM的最小值.
考点:轴对称-最短路线问题,等边三角形的性质
专题:数形结合
分析:作出A关于BC的对称点A',将PA+PM的最小值问题转化为两点之间线段最短的问题,并利用等边三角形的性质和勾股定理解答.
解答: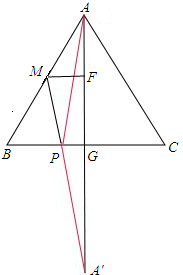 解:作A关于BC的对称点A',连接MA',作MF⊥AG.
解:作A关于BC的对称点A',连接MA',作MF⊥AG.
∵A、A'关于BC对称,
∴PA=PA',
∴PA+PM=PA'+PM=MA',
此时MA'的值即为PA+PM的最小值.
∵AG⊥BC,
又∵△ABC为等边三角形,
∴BG=CG=
BC=
×2=1.
∴AG=
=
.
∵M为AB的中点,MF⊥AG,
∴MF为△ABG的中位线,
∴MF=
BG=
,FG=
AG=
×
=
,FA'=FG+GA'=
+
=
,
∴A'M=
=
.
 解:作A关于BC的对称点A',连接MA',作MF⊥AG.
解:作A关于BC的对称点A',连接MA',作MF⊥AG.∵A、A'关于BC对称,
∴PA=PA',
∴PA+PM=PA'+PM=MA',
此时MA'的值即为PA+PM的最小值.
∵AG⊥BC,
又∵△ABC为等边三角形,
∴BG=CG=
| 1 |
| 2 |
| 1 |
| 2 |
∴AG=
| 22-12 |
| 3 |
∵M为AB的中点,MF⊥AG,
∴MF为△ABG的中位线,
∴MF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| ||
| 2 |
3
| ||
| 2 |
∴A'M=
(
|
| 7 |
点评:此题结合等边三角形的性质考查了轴对称最短路径问题,作出A的对称点利用轴对称的性质和勾股定理是解题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
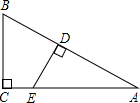 如图,Rt△ABC中,∠C=90°,∠A=30°,点D、E分别在AB、AC上,且DE⊥AB,若DE将△ABC分成面积相等的两部分,那么线段CE与AE的长度的比是
如图,Rt△ABC中,∠C=90°,∠A=30°,点D、E分别在AB、AC上,且DE⊥AB,若DE将△ABC分成面积相等的两部分,那么线段CE与AE的长度的比是