题目内容
11.已知二次函数y=ax2+bx+c(a>0)的图象经过点A(-1,2),B(2,5),顶点坐标为(m,n),则下列说法错误的是( )| A. | c<3 | B. | b<1 | C. | n≤2 | D. | m>$\frac{1}{2}$ |
分析 根据已知条件得到$\left\{\begin{array}{l}{a-b+c=2}\\{4a+2b+c=5}\end{array}\right.$,解方程组得到c=3-2a<3,b=1-a<1,求得二次函数的对称轴为x=-$\frac{b}{2a}$=-$\frac{1-a}{2a}$=$\frac{1}{2}$-$\frac{1}{2a}$<$\frac{1}{2}$,根据二次函数的顶点坐标即可得到结论.
解答 解:由已知可知:$\left\{\begin{array}{l}{a-b+c=2}\\{4a+2b+c=5}\end{array}\right.$,
消去b得:c=3-2a<3,
消去c得:b=1-a<1,
对称轴:x=-$\frac{b}{2a}$=-$\frac{1-a}{2a}$=$\frac{1}{2}$-$\frac{1}{2a}$<$\frac{1}{2}$,
∵A(-1,2),a>0,那么顶点的纵坐标为函数的最小值,
∴n≤2,
故D错误.
故选:D.
点评 本题考查了二次函数的性质,二次函数图象上点的坐标特征,熟记二次函数的性质是解题的关键.

练习册系列答案
相关题目
1.下列图形中,不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
2.下列运算正确的是( )
| A. | (2a)2=2a2 | B. | a6÷a2=a3 | C. | (a+b)2=a2+b2 | D. | a3•a2=a5 |
6.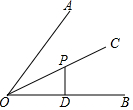 如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
 如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )
如图,点P是∠AOB平分线OC上一点,PD⊥OB,垂足为D,若PD=2,则点P到边OA的距离是( )| A. | 1 | B. | 2 | C. | $\sqrt{3}$ | D. | 4 |
16.某种商品一周内卖出的件数从周一到周日统计如下:26,36,22,22,24,31,21,关于这组数据,下列说法错误的是( )
| A. | 方差是21 | B. | 平均数是26 | C. | 众数是22 | D. | 中位数是24 |
20.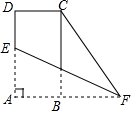 如图,在矩形ABCD中,AD=2,AB=1,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠CFE的正切值为( )
如图,在矩形ABCD中,AD=2,AB=1,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠CFE的正切值为( )
 如图,在矩形ABCD中,AD=2,AB=1,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠CFE的正切值为( )
如图,在矩形ABCD中,AD=2,AB=1,点E在AD上,F为AB延长线上一点,将△AEF沿EF翻折,点A恰好与点C重合,则∠CFE的正切值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
 如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为5.
如图,AB为⊙O的直径,弦CD⊥AB于点E,已知CD=6,EB=1,则⊙O的半径为5.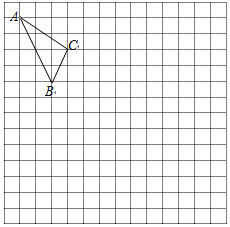 在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-4,6),(-1,4).
在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-4,6),(-1,4).