题目内容
1.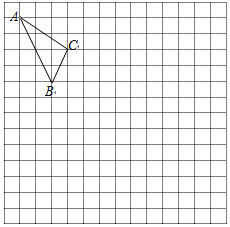 在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-4,6),(-1,4).
在如图的正方形网格中,每一个小正方形的边长为1.格点三角形ABC(顶点是网格线交点的三角形)的顶点A、C的坐标分别是(-4,6),(-1,4).(1)请在图中的网格平面内建立平面直角坐标系;
(2)请画出△ABC关于x轴对称的△A1B1C1;
(3)请在y轴上求作一点P,使△PB1C的周长最小,并写出点P的坐标.
分析 (1)根据A点坐标建立平面直角坐标系即可;
(2)分别作出各点关于x轴的对称点,再顺次连接即可;
(3)作出点B关于y轴的对称点B2,连接A、B2交y轴于点P,则P点即为所求.
解答 解:(1)如图所示;
(2)如图,即为所求;
(3)作点B1关于y轴的对称点B2,连接C、B2交y轴于点P,则点P即为所求.
设直线CB2的解析式为y=kx+b(k≠0),
∵C(-1,4),B2(2,-2),
∴$\left\{\begin{array}{l}{-k+b=4}\\{2k+b=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-2}\\{b=2}\end{array}\right.$,
∴直线AB2的解析式为:y=-2x+2,
∴当x=0时,y=2,
∴P(0,2).
点评 本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
11.已知二次函数y=ax2+bx+c(a>0)的图象经过点A(-1,2),B(2,5),顶点坐标为(m,n),则下列说法错误的是( )
| A. | c<3 | B. | b<1 | C. | n≤2 | D. | m>$\frac{1}{2}$ |
16.点A、B分别是函数y=$\frac{4}{x}$(x>0)和y=-$\frac{4}{x}$(x<0)图象上的一点,A、B两点的横坐标分别为a、b,且OA=OB,a+b≠0,则ab的值为( )
| A. | 2 | B. | -2 | C. | 4 | D. | -4 |
6.某商店今年1月份的销售额是2万元,3月份的销售额是4.5万元,从1月份到3月份,该店销售额平均每月的增长率是( )
| A. | 20% | B. | 25% | C. | 50% | D. | 62.5% |
13.下表是一组二次函数y=x2+3x-5的自变量x与函数值y的对应值:
那么方程x2+3x-5=0的一个近似根是( )
| x | 1 | 1.1 | 1.2 | 1.3 | 1.4 |
| y | -1 | -0.49 | 0.04 | 0.59 | 1.16 |
| A. | 1 | B. | 1.1 | C. | 1.2 | D. | 1.3 |
10.一组数据:5,4,6,5,6,6,3,这组数据的众数是( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |