题目内容
10. 填空:把下面的推理过程补充完整,并在括号内注明理由.
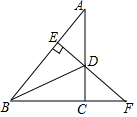
填空:把下面的推理过程补充完整,并在括号内注明理由.如图,在Rt△ABC中,∠ACB=90°,BD是∠ABC的平分线,DE⊥AB.垂足为E,ED的延长线交BC的延长线于点F.
求证:AE=CF,∠A=∠F
证明:∵∠ACB=90°(已知)
∴DC⊥BC(垂直的定义)
又∵BD为∠ABC的平分线,DE⊥AB,(已知)
∴DC=DE (角平分线的性质)
∵在△ADE和△FDC中
∠DEA=∠DCF=90° (垂直的定义)
DE=DC(已证)
∠ADE=∠FDC(对顶角相等)
∴△ADE≌△FDC(ASA)
∴AE=CF (全等三角形的对应边相等)
∠A=∠F (全等三角形的对应角相等).
分析 由角平分线的性质可求得DC=DE,则可证得△ADE≌△FDC,再利用全等三角形的性质可证得结论,据此填空即可.
解答 证明:
∵∠ACB=90°(已知),
∴DC⊥BC(垂直的定义),
又∵BD为∠ABC的平分线,DE⊥AB,(已知),
∴DC=DE (角平分线的性质),
∵在△ADE和△FDC中,
∠DEA=∠DCF=90° (垂直的定义),
DE=DC(已证),
∠ADE=∠FDC(对顶角相等),
∴△ADE≌△FDC(ASA),
∴AE=CF (全等三角形的对应边相等),
∠A=∠F (全等三角形的对应角相等).
故答案为:角平分线的性质;已证;对顶角相等;ASA;全等三角形的对应边相等;全等三角形的对应角相等.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法(即SSS、SAS、ASA、AAS和HL)和全等三角形的性质(对应边相等、对应角相等)是解题的关键.

练习册系列答案
相关题目
1.某商场销售A、B两种商品,这两种商品的进价和售价如表所示,该商场计划购进两种商品若干,共需66万元,全部销售后可获利润9万元.
(1)该商场计划购进A、B两种商品各多少件?;
(2)通过市场调研,该商场决定在原计划的基础上,减少A种商品的购进数量,增加B种商品的购进数量,已知B种商品增加的数量是A种商品减少的数量的1.5倍.若用于购进这两种商品的总资金不超过69万.问A种商品购进数至多减少多少件?
| A | B | |
| 进价(万元/件) | 1.5 | 1.2 |
| 售价(万元/件) | 1.65 | 1.4 |
(2)通过市场调研,该商场决定在原计划的基础上,减少A种商品的购进数量,增加B种商品的购进数量,已知B种商品增加的数量是A种商品减少的数量的1.5倍.若用于购进这两种商品的总资金不超过69万.问A种商品购进数至多减少多少件?
18.下列方程中关于x的一元二次方程的是( )
| A. | 3(x+1)2=2(x+1) | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$=2 | C. | x2+2x=x2-1 | D. | ax2+bx+c=0 |
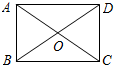 如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的边长BC的长是2$\sqrt{3}$.
如图,矩形ABCD的两条对角线相交于点O,∠AOB=60°,AB=2,则矩形的边长BC的长是2$\sqrt{3}$.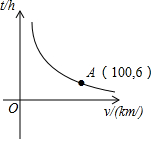 一辆汽车从甲地开往乙地,随着汽车平均速度v(km/h)的变化,所需时间t(h)
一辆汽车从甲地开往乙地,随着汽车平均速度v(km/h)的变化,所需时间t(h) 已知线段AB=8,延长AB到C,使BC=6.如果点D是线段AB的中点,点E是线段BC的中点,那么线段DE的长度是多少?(自己将图补充完整并请写出求解过程)
已知线段AB=8,延长AB到C,使BC=6.如果点D是线段AB的中点,点E是线段BC的中点,那么线段DE的长度是多少?(自己将图补充完整并请写出求解过程) 如图,在平面直角坐标系中,已知长方形ABCD的两个顶点坐标为A(2,-1),C(6,2),AB∥x轴,点M为y轴上一点,△MAB的面积为6,且MD<MA;
如图,在平面直角坐标系中,已知长方形ABCD的两个顶点坐标为A(2,-1),C(6,2),AB∥x轴,点M为y轴上一点,△MAB的面积为6,且MD<MA;