题目内容
3. 如图,在平面直角坐标系中,已知长方形ABCD的两个顶点坐标为A(2,-1),C(6,2),AB∥x轴,点M为y轴上一点,△MAB的面积为6,且MD<MA;
如图,在平面直角坐标系中,已知长方形ABCD的两个顶点坐标为A(2,-1),C(6,2),AB∥x轴,点M为y轴上一点,△MAB的面积为6,且MD<MA;请解答下列问题:
(1)顶点B的坐标为(6,-1);
(2)求点M的坐标;
(3)在△MAB中任意一点P(x0,y0)经平移后对应点为P1(x0-5,y0-1),将△MAB作同样的平移得到△M1A1B1,则点M1的坐标为(-5,1).
分析 (1)根据矩形的性质,以及A、C两点的坐标即可解决问题;
(2)设M(0,m),由题意$\frac{1}{2}$×4×|m+1|=6,求出m的值即可判断;
(3)将点M(0,2)向左平移5个单位,向下平移1好单位得到M1(-5,1);
解答 解:(1) ∵A(2,-1),C(6,2),AB∥x轴,四边形ABCD是矩形,
∵A(2,-1),C(6,2),AB∥x轴,四边形ABCD是矩形,
∴B(6,-1).
故答案为(6,-1).
(2)设M(0,m),
由题意$\frac{1}{2}$×4×|m+1|=6,
解得m=2或-3,
∴M(0,2)或(0,-3)(舍弃不合题意).
(3)将点M(0,2)向左平移5个单位,向下平移1好单位得到M1(-5,1),
故答案为(-5,1).
点评 本题考查矩形的性质、坐标与图形的性质、平移变换等知识,解题的关键是灵活运用所学知识解决问题,学会构建方程解决问题.

练习册系列答案
相关题目
13.下列运算错误的是( )
| A. | a+2a=3a | B. | (a2)3=a6 | C. | a2•a3=a5 | D. | a6÷a3=a2 |
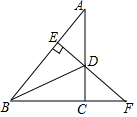 填空:把下面的推理过程补充完整,并在括号内注明理由.
填空:把下面的推理过程补充完整,并在括号内注明理由.
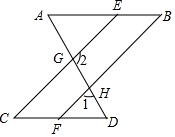 如图,已知∠A=∠AGE,∠D=∠DGC.
如图,已知∠A=∠AGE,∠D=∠DGC. 如图,有下列判断①∠1与∠3是对顶角②∠1与∠4是内错角③∠1与∠2是同旁内角④∠3与∠4是同位角,其中不正确的是( )
如图,有下列判断①∠1与∠3是对顶角②∠1与∠4是内错角③∠1与∠2是同旁内角④∠3与∠4是同位角,其中不正确的是( )