题目内容
19.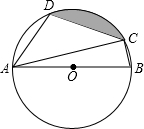 如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=108°,连接AC.
如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=108°,连接AC.(1)求∠BAC的度数;
(2)若∠DCA=27°,AB=8,求图中阴影部分的面积(结果保留π).
分析 (1)根据圆内接四边形的性质得到∠B=72°,根据AB是⊙O的直径,得到∠ACB=90°,根据三角形的内角和即可得到结论;
(2)连接OC,OD,根据三角形的内角和得到∠DAC=180°-108°-27°=45°,由圆周角定理得到∠DOC=90°,推出△COD是等腰直角三角形,根据扇形和三角形的面积公式即可得到结论.
解答 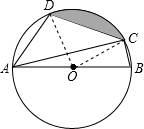 解:(1)∵四边形ABCD是⊙O的内接四边形,∠D=108°,
解:(1)∵四边形ABCD是⊙O的内接四边形,∠D=108°,
∴∠B=72°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=18°;
(2)连接OC,OD,
∵∠D=108°,∠DCA=27°,
∴∠DAC=180°-108°-27°=45°,
∴∠DOC=90°,
∴△COD是等腰直角三角形,
∵AB=8,
∴OC=OD=4,
∴阴影部分的面积=S扇形COD-S△COD=$\frac{90π×{4}^{2}}{360}$-$\frac{1}{2}$×42=4π-8.
点评 本题考查了圆内接四边形的性质,圆周角定理,等腰直角三角形的判定和性质,扇形的面积的计算,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
10.为了了解某校八年级1000名学生的身高,从中抽取了50名学生并对他们的身高进行统计分析,以下说法正确的是( )
| A. | 1 000名学生是总体 | |
| B. | 抽取的50名学生是样本容量 | |
| C. | 每位学生的身高是个体 | |
| D. | 被抽取的50名学生是总体的一个样本 |
7.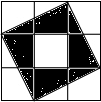 小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )
小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )
 小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )
小明把如图所示的3×3的正方形网格纸板挂在墙上玩飞镖游戏(每次飞镖均落在纸板上,且落在纸板的任何一个点的机会都相等),则飞镖落在阴影区域(四个全等的直角三角形的每个顶点都在格点上)的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
8.小明从一副扑克牌中取出3张红桃、2张黑桃共5张牌与弟弟做游戏,把这5张牌背面朝上洗匀后放在桌子上,小明与弟弟同时各抽一张,两人抽到花色相同的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{5}$ |
 如图,菱形ABCD的周长为16,∠B=60°,则以AC为边长的正方形ACEF的周长为16.
如图,菱形ABCD的周长为16,∠B=60°,则以AC为边长的正方形ACEF的周长为16.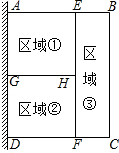 如图,某小区准备用篱笆围成一块矩形花圃ABCD,为了节省篱笆,一边利用足够长的墙,另外三边用篱笆围着,再用两段篱笆EF与GH将矩形ABCD分割成①②③三块矩形区域,而且这三块矩形区域的面积相等,现有总长80m的篱笆,当围成的花圃ABCD的面积最大时,AB的长为15m.
如图,某小区准备用篱笆围成一块矩形花圃ABCD,为了节省篱笆,一边利用足够长的墙,另外三边用篱笆围着,再用两段篱笆EF与GH将矩形ABCD分割成①②③三块矩形区域,而且这三块矩形区域的面积相等,现有总长80m的篱笆,当围成的花圃ABCD的面积最大时,AB的长为15m.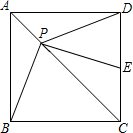 如图,边长为1的正方形ABCD中,P为对角线AC上的任意一点,分别连接PB、PD,
如图,边长为1的正方形ABCD中,P为对角线AC上的任意一点,分别连接PB、PD,



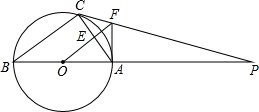 如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P.OF∥BC交AC于点E,交PC于点F,连结AF.
如图,△ABC内接于⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P.OF∥BC交AC于点E,交PC于点F,连结AF.