题目内容
4.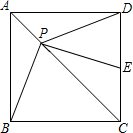 如图,边长为1的正方形ABCD中,P为对角线AC上的任意一点,分别连接PB、PD,
如图,边长为1的正方形ABCD中,P为对角线AC上的任意一点,分别连接PB、PD,PE⊥PB,交CD与E.
(1)求证:PE=PD;
(2)当E为CD的中点时,求AP的长;
(3)设AP=x(0<x<$\frac{\sqrt{2}}{2}$),四边形BPEC的面积为y,求证:y=$\frac{1}{2}$($\sqrt{2}$-x)2.
分析 (1)作PG⊥BC于G,PH⊥CD于H,根据轴对称图形的性质得到PB=PD,PG=PH,证明△BPG≌△EPH,得到PB=PE,等量代换得到答案;
(2)证明∠DPH=∠EPH,根据等腰三角形的性质求出DH,根据勾股定理计算即可;
(3)根据四边形BPEC的面积=正方形PGCH的面积计算.
解答 (1)证明: 作PG⊥BC于G,PH⊥CD于H,
作PG⊥BC于G,PH⊥CD于H,
∵四边形ABCD是正方形,正方形是轴对称图形,
∴PB=PD,PG=PH,∠BCD=90°,
∴四边形PGCH是矩形,
∴PG⊥PH,又PE⊥PB,
∴∠BPG=∠EPH,
在△BPG和△EPH中,
$\left\{\begin{array}{l}{∠BPG=∠EPH}\\{PG=PH}\\{∠PGB=∠PHE}\end{array}\right.$,
∴△BPG≌△EPH,
∴PB=PE,又PB=PD,
∴PE=PD;
(2)解:∵四边形ABCD是轴对称图形,
∴∠BPC=∠DPC,∠GPC=∠HPC=45°,
∴∠BPG=∠DPH,又∠BPG=∠EPH,
∴∠DPH=∠EPH,又PH⊥CD,
∴DH=EH=$\frac{1}{2}$DE=$\frac{1}{4}$CD=$\frac{1}{4}$,
∴PH=HC=$\frac{3}{4}$,
∴PC=$\frac{3\sqrt{2}}{4}$,
∵正方形ABCD的边长为1,
∴AC=$\sqrt{2}$,
∴AP=AC-PC=$\frac{\sqrt{2}}{4}$;
(3)证明:∵AC=$\sqrt{2}$,AP=x,
∴PC=$\sqrt{2}$-x,
∵△BPG≌△EPH,
∴四边形BPEC的面积y=正方形PGCH的面积=$\frac{1}{2}$($\sqrt{2}$-x)2.
点评 本题考查的是正方形的性质、全等三角形的判定和性质,掌握正方形的四条边相等、四个角都是90°、一条对角线平分一组对角是解题的关键.

| A. | 3a3+4a3=7a6 | B. | 3a2•4a2=12a2 | C. | (a+2)2=a2+4 | D. | (a+b)(a-b)=a2-b2 |
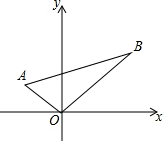 如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )
如图,在平面直角坐标系中,Rt△AOB的直角顶点与原点O重合,顶点A的坐标为(-1,1),∠ABO=30°,若顶点B在第一象限,则点B的坐标为( )| A. | (1,1) | B. | ($\sqrt{2}$,$\sqrt{2}$) | C. | ($\sqrt{3}$,$\sqrt{3}$) | D. | (2,2) |
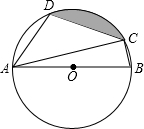 如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=108°,连接AC.
如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,∠D=108°,连接AC. 如图,已知AD∥BE∥CF,$\frac{AB}{BC}=\frac{2}{3}$,DE=3,则DF的长为7.5.
如图,已知AD∥BE∥CF,$\frac{AB}{BC}=\frac{2}{3}$,DE=3,则DF的长为7.5.