题目内容
2.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共30只,某小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 | … |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 | … |
| 摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 | … |
(2)假如你去摸一次,你摸到白球的概率是0.60,摸到黑球的概率是0.40;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
分析 (1)本题需先根据表中的数据,估计出摸到白球的频率.
(2)本题根据摸到白球的频率即可求出摸到白球和黑球的概率.
(3)根据口袋中黑、白两种颜色的球的概率即可求出口袋中黑、白两种颜色的球有多少只.
解答 答:(1)根据题意可得当n很大时,摸到白球的频率将会接近0.60;
(2)因为当n很大时,摸到白球的频率将会接近0.60;
所以摸到白球的概率是0.6;
摸到黑球的概率是0.4;
(3)因为摸到白球的概率是0.6,摸到黑球的概率是0.4,
所以口袋中黑、白两种颜色的球有白球是30×0.6=18个,
黑球是30×0.4=12个;
故答案为:(1)0.60;
(2)0.6,0.4;
点评 本题主要考查了如何利用频率估计概率,在解题时要注意频率和概率之间的关系.

练习册系列答案
相关题目
12.下列计算中,正确的是( )
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | D. | $\sqrt{8}$÷$\sqrt{2}$=4 |
7.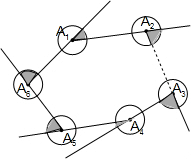 如图所示,分别以n边形的顶点为圆心,以1cm为半径画园,当n=2017时则图中阴影部分的面积之和为( )
如图所示,分别以n边形的顶点为圆心,以1cm为半径画园,当n=2017时则图中阴影部分的面积之和为( )
 如图所示,分别以n边形的顶点为圆心,以1cm为半径画园,当n=2017时则图中阴影部分的面积之和为( )
如图所示,分别以n边形的顶点为圆心,以1cm为半径画园,当n=2017时则图中阴影部分的面积之和为( )| A. | πcm2 | B. | 2πcm2 | C. | 2016πcm2 | D. | 2017πcm2 |