题目内容
12.计算:$\frac{x}{{x}^{2}y-y}$÷$\frac{xy}{{x}^{2}+x}$=$\frac{x}{{y}^{2}x-{y}^{2}}$.分析 直接利用分式的除法运算法则计算得出答案.
解答 解:$\frac{x}{{x}^{2}y-y}$÷$\frac{xy}{{x}^{2}+x}$=$\frac{x}{y(x+1)(x-1)}$×$\frac{x(x+1)}{xy}$
=$\frac{x}{{y}^{2}x-{y}^{2}}$.
故答案为:$\frac{x}{{y}^{2}x-{y}^{2}}$.
点评 此题主要考查了分式的除法运算,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
2.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共30只,某小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近0.60;
(2)假如你去摸一次,你摸到白球的概率是0.60,摸到黑球的概率是0.40;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 | … |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 | … |
| 摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 | … |
(2)假如你去摸一次,你摸到白球的概率是0.60,摸到黑球的概率是0.40;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
20.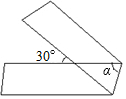 如图,有一条长方形的宽纸带,按图折叠,则∠α=( )
如图,有一条长方形的宽纸带,按图折叠,则∠α=( )
 如图,有一条长方形的宽纸带,按图折叠,则∠α=( )
如图,有一条长方形的宽纸带,按图折叠,则∠α=( )| A. | 30° | B. | 60° | C. | 70° | D. | 75° |
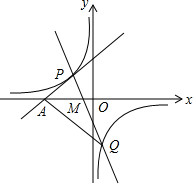 如图所示,P(a,3)是直线y=x+5上的一点,直线 y=k1x+b与双曲线y=$\frac{k}{x}$相交于P、Q(1,m).
如图所示,P(a,3)是直线y=x+5上的一点,直线 y=k1x+b与双曲线y=$\frac{k}{x}$相交于P、Q(1,m).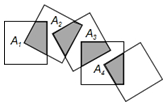 如图,将n个边长都为1cm的正方形按如图所示摆放,点A1,A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为$\frac{n-1}{4}$cm2.
如图,将n个边长都为1cm的正方形按如图所示摆放,点A1,A2,…,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为$\frac{n-1}{4}$cm2.