题目内容
11.如果$\left\{\begin{array}{l}x=2\\ y=2\end{array}\right.$是方程组$\left\{\begin{array}{l}x+y=a\\ 2x-y=b+1\end{array}\right.$的解,则a-b=3.分析 先根据$\left\{\begin{array}{l}x=2\\ y=2\end{array}\right.$是方程组$\left\{\begin{array}{l}x+y=a\\ 2x-y=b+1\end{array}\right.$的解,得到$\left\{\begin{array}{l}{2+2=a}\\{4-2=b+1}\end{array}\right.$,进而得到$\left\{\begin{array}{l}{a=4}\\{b=1}\end{array}\right.$,据此可得结论.
解答 解:∵$\left\{\begin{array}{l}x=2\\ y=2\end{array}\right.$是方程组$\left\{\begin{array}{l}x+y=a\\ 2x-y=b+1\end{array}\right.$的解,
∴$\left\{\begin{array}{l}{2+2=a}\\{4-2=b+1}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=4}\\{b=1}\end{array}\right.$,
∴a-b=4-1=3,
故答案为:3.
点评 本题主要考查了二元一次方程组的解,解题时注意:当遇到有关二元一次方程组的解的问题时,通常采用代入法,即将解代入原方程组,这种方法主要用在求方程中的字母系数.

练习册系列答案
相关题目
2.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共30只,某小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近0.60;
(2)假如你去摸一次,你摸到白球的概率是0.60,摸到黑球的概率是0.40;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 | … |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 | … |
| 摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 | … |
(2)假如你去摸一次,你摸到白球的概率是0.60,摸到黑球的概率是0.40;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
16.下列运算正确的是( )
| A. | $\root{3}{-1}=-\root{3}{-1}$ | B. | $\root{3}{-3}=\root{3}{3}$ | C. | $\root{3}{-1}=\root{3}{{|{-1}|}}$ | D. | $\root{3}{-1}=-\root{3}{1}$ |
20.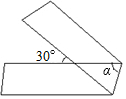 如图,有一条长方形的宽纸带,按图折叠,则∠α=( )
如图,有一条长方形的宽纸带,按图折叠,则∠α=( )
 如图,有一条长方形的宽纸带,按图折叠,则∠α=( )
如图,有一条长方形的宽纸带,按图折叠,则∠α=( )| A. | 30° | B. | 60° | C. | 70° | D. | 75° |

 如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数.
如图,AB∥DE,∠B=80°,CM平分∠BCD,CN⊥CM,求∠NCE的度数. 如图,正方形ABCD的边长为10,在正方形ABCD内有一点E,满足∠AEB=90°,AE=6,求阴影部分的面积.
如图,正方形ABCD的边长为10,在正方形ABCD内有一点E,满足∠AEB=90°,AE=6,求阴影部分的面积.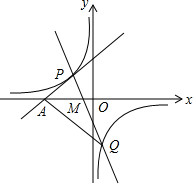 如图所示,P(a,3)是直线y=x+5上的一点,直线 y=k1x+b与双曲线y=$\frac{k}{x}$相交于P、Q(1,m).
如图所示,P(a,3)是直线y=x+5上的一点,直线 y=k1x+b与双曲线y=$\frac{k}{x}$相交于P、Q(1,m).