题目内容
13.(1)计算-2+(π-5)0+(-2)-3(2)解方程组$\left\{\begin{array}{l}{x=y+1}\\{4x-3y=5}\end{array}\right.$.
分析 (1)原式利用零指数幂、负整数指数幂法则计算即可得到结果;
(2)方程组利用代入消元法求出解即可.
解答 解:(1)-2+(π-5)0+(-2)-3
=-2+1+(-$\frac{1}{8}$)
=-$\frac{9}{8}$;
(2)$\left\{\begin{array}{l}{x=y+1①}\\{4x-y=5②}\end{array}\right.$,
将①代入②,得4(y+1)-3y=5,
解这个一元二次方程,得y=1,
将y=1代入①,得x=2,
则原方程的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
8.20162-2017×2015的计算结果是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 4030 |
5.△ABC的三边分别为下列各组值,其中不是直角三角形三边的是( )
| A. | a=13,b=12,c=5 | B. | a=1.2,b=1.6,c=2 | C. | a=$\frac{1}{3}$,b=$\frac{1}{4}$,c=$\frac{1}{5}$ | D. | a=$\frac{4}{3}$,b=$\frac{5}{3}$,c=1 |
2.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共30只,某小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近0.60;
(2)假如你去摸一次,你摸到白球的概率是0.60,摸到黑球的概率是0.40;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 | … |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 | … |
| 摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 | … |
(2)假如你去摸一次,你摸到白球的概率是0.60,摸到黑球的概率是0.40;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
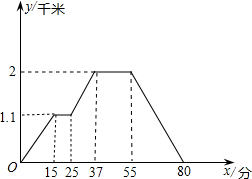 下面的图象反映的过程是:小明从家去超市买文具,又去书店购书,然后回家,其中x表示时间,y表示小明离他家的距离,且小明家、超市、书店在同一直线上.根据图象回答下列问题:
下面的图象反映的过程是:小明从家去超市买文具,又去书店购书,然后回家,其中x表示时间,y表示小明离他家的距离,且小明家、超市、书店在同一直线上.根据图象回答下列问题:
 如图,平行四边形ABCD中,E、F是对角线BD上的两点,在不添加任何辅助线的情况下,如果添加一个条件使△ABE≌△CDF,则添加的条件是BE=FD或BF=DE或∠1=∠2(答案不唯一).
如图,平行四边形ABCD中,E、F是对角线BD上的两点,在不添加任何辅助线的情况下,如果添加一个条件使△ABE≌△CDF,则添加的条件是BE=FD或BF=DE或∠1=∠2(答案不唯一).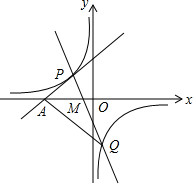 如图所示,P(a,3)是直线y=x+5上的一点,直线 y=k1x+b与双曲线y=$\frac{k}{x}$相交于P、Q(1,m).
如图所示,P(a,3)是直线y=x+5上的一点,直线 y=k1x+b与双曲线y=$\frac{k}{x}$相交于P、Q(1,m).