题目内容
12.下列计算中,正确的是( )| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | C. | $\sqrt{2}$×$\sqrt{5}$=$\sqrt{10}$ | D. | $\sqrt{8}$÷$\sqrt{2}$=4 |
分析 根据二次根式的加减法对A、B进行判断;根据二次根式的乘法法则对C进行判断;根据二次根式的除法法则对D进行判断.
解答 解:A、原式=2$\sqrt{2}$-$\sqrt{2}$=$\sqrt{2}$,所以A选项计算错误;
B、$\sqrt{2}$与$\sqrt{3}$不能合并,所以B选项计算错误;
C、原式=$\sqrt{2×5}$=$\sqrt{10}$,所以C选项计算正确;
D、原式=$\sqrt{8÷4}$=$\sqrt{2}$,所以D选项计算错误.
故选C.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
2.在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共30只,某小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
(1)请估计:当n很大时,摸到白球的频率将会接近0.60;
(2)假如你去摸一次,你摸到白球的概率是0.60,摸到黑球的概率是0.40;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 | … |
| 摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 | … |
| 摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 | … |
(2)假如你去摸一次,你摸到白球的概率是0.60,摸到黑球的概率是0.40;
(3)试估算口袋中黑、白两种颜色的球各有多少只?
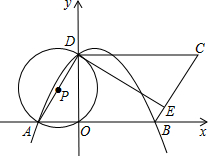 如图,在平面直角坐标系xoy中,O为原点,?ABCD的边AB在x轴上,点D在y轴上,点A的坐标为(-2,0),AB=6,∠BAD=60°,点E是BC边上一点,CE=3EB,⊙P过A、O、D三点,抛物线y=ax2+bx+c过点A、B、D三点.
如图,在平面直角坐标系xoy中,O为原点,?ABCD的边AB在x轴上,点D在y轴上,点A的坐标为(-2,0),AB=6,∠BAD=60°,点E是BC边上一点,CE=3EB,⊙P过A、O、D三点,抛物线y=ax2+bx+c过点A、B、D三点.
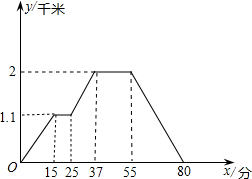 下面的图象反映的过程是:小明从家去超市买文具,又去书店购书,然后回家,其中x表示时间,y表示小明离他家的距离,且小明家、超市、书店在同一直线上.根据图象回答下列问题:
下面的图象反映的过程是:小明从家去超市买文具,又去书店购书,然后回家,其中x表示时间,y表示小明离他家的距离,且小明家、超市、书店在同一直线上.根据图象回答下列问题: