题目内容
11. 把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m厘米,宽为n厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m厘米,宽为n厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )| A. | 4n厘米 | B. | 4m厘米 | C. | 2(m+n)厘米 | D. | 4(m+n)厘米 |
分析 设图①小长方形的长为a,宽为b,由图②表示出上面与下面两个长方形的周长,求出之和,根据题意得到a+2b=m,代入计算即可得到结果.
解答 解:设小长方形的长为a,宽为b,
上面的长方形周长:2(m-a+n-a),下面的长方形周长:2(m-2b+n-2b),
两式联立,总周长为:2(m-a+n-a)+2(m-2b+n-2b)=4m+4n-4(a+2b),
∵a+2b=m(由图可得),
∴阴影部分总周长为4m+4n-4(a+2b)=4m+4n-4m=4n(厘米).
故选A.
点评 此题考查了整式的加减,熟练掌握运算法则是解本题的关键.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
7.下列关于反比例函数y=$\frac{k-1}{x}$的说法中,不正确的是( )
| A. | 该反比例函数的图象与坐标轴无交点 | |
| B. | 当k>0时,该反比例函数的图象在第一、三象限 | |
| C. | 如果该反比例函数的图象过点(1,3),那么也一定过点(-1,-3) | |
| D. | 当y随x的增大而减小时,k>1 |
20.下列算式正确的是( )
| A. | (a+b)2=a2+b2 | B. | (-a)6÷(-a)2=-a3 | ||
| C. | (-a-b)2=(a+b)2 | D. | (-4a-1)(4a-1)=16a2-1 |
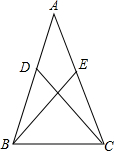 如图,在△ABC中,点D、点E分别在AB、AC上,连接BE、CD,现有下列三个式子:?①AB=AC,?②BD=CE,③?CD=BE.请从三个式子中选两个合适的式子作为已知条件,剩下的一个式子作为待说明成立的结论,并说明该结论的正确性.
如图,在△ABC中,点D、点E分别在AB、AC上,连接BE、CD,现有下列三个式子:?①AB=AC,?②BD=CE,③?CD=BE.请从三个式子中选两个合适的式子作为已知条件,剩下的一个式子作为待说明成立的结论,并说明该结论的正确性. 如图所示,是由若干个相同的小正方体搭成的几何体的三视图,该几何体由多少个小正方体搭成6.
如图所示,是由若干个相同的小正方体搭成的几何体的三视图,该几何体由多少个小正方体搭成6. 如图,在△ADF与△CBE中,点A、E、F、C在同一直线上,已知AD∥BC,AD=CB,∠B=∠D.求证:△ADF≌△CBE.
如图,在△ADF与△CBE中,点A、E、F、C在同一直线上,已知AD∥BC,AD=CB,∠B=∠D.求证:△ADF≌△CBE. 已知:在平行四边形ABCD中,O是对角线BD的中点,P为线段BC上一点,连接PO并延长交AD于点Q,求证:OP=OQ.
已知:在平行四边形ABCD中,O是对角线BD的中点,P为线段BC上一点,连接PO并延长交AD于点Q,求证:OP=OQ.