题目内容
6.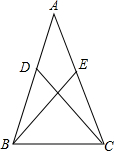 如图,在△ABC中,点D、点E分别在AB、AC上,连接BE、CD,现有下列三个式子:?①AB=AC,?②BD=CE,③?CD=BE.请从三个式子中选两个合适的式子作为已知条件,剩下的一个式子作为待说明成立的结论,并说明该结论的正确性.
如图,在△ABC中,点D、点E分别在AB、AC上,连接BE、CD,现有下列三个式子:?①AB=AC,?②BD=CE,③?CD=BE.请从三个式子中选两个合适的式子作为已知条件,剩下的一个式子作为待说明成立的结论,并说明该结论的正确性.解答:我选择已知:①②,结论:③.(只需要填序号)
分析 根据全等三角形的各种判断方法选择已知和要求证的结论即可,此题答案不唯一.
解答 解:已知:①②,
结论:③,
理由如下:
∵AB=AC,
∴∠ABC=∠ACB,
在△DBC和△ECB中,
$\left\{\begin{array}{l}{BD=CE}\\{∠DBC=∠ECB}\\{BC=CB}\end{array}\right.$,
∴△DBC≌△ECB,
∴BE=CD.
故答案为:①②,③.
点评 本题考查了全等三角形的判断和性质,熟记全等三角形的各种判断方法以及各种性质是解题的关键.

练习册系列答案
相关题目
11. 把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m厘米,宽为n厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m厘米,宽为n厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
 把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m厘米,宽为n厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m厘米,宽为n厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )| A. | 4n厘米 | B. | 4m厘米 | C. | 2(m+n)厘米 | D. | 4(m+n)厘米 |
 小梅用两张同样大小的长方形硬纸片拼接成一个面积为900cm2的正方形,如图所示,按要求完成下列各小题.
小梅用两张同样大小的长方形硬纸片拼接成一个面积为900cm2的正方形,如图所示,按要求完成下列各小题.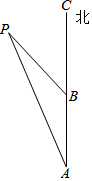 如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,2小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,求此时轮船和小岛的距离.
如图,一艘轮船从点A向正北方向航行,每小时航行15海里,小岛P在轮船的北偏西15°,2小时后轮船航行到点B,小岛P此时在轮船的北偏西30°方向,求此时轮船和小岛的距离.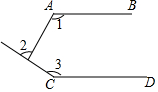 如图,已知AB∥CD,∠1=115°,∠3=140°,则∠2=75°.
如图,已知AB∥CD,∠1=115°,∠3=140°,则∠2=75°.