题目内容
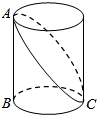 如图,已知圆柱底面的周长为2m,圆柱高为1m,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为
如图,已知圆柱底面的周长为2m,圆柱高为1m,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的周长最小为考点:平面展开-最短路径问题
专题:
分析:要求丝线的长,需将圆柱的侧面展开,进而根据“两点之间线段最短”得出结果,在求线段长时,根据勾股定理计算即可.
解答: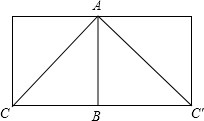 解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
∵圆柱底面的周长为2m,圆柱高为1m,
∴AB=1m,BC=BC′=1m,
∴AC2=12+12=2,
∴AC=
m,
∴这圈金属丝的周长最小为2AC=2
m.
故答案为:2
m.
 解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.
解:如图,把圆柱的侧面展开,得到矩形,则这圈金属丝的周长最小为2AC的长度.∵圆柱底面的周长为2m,圆柱高为1m,
∴AB=1m,BC=BC′=1m,
∴AC2=12+12=2,
∴AC=
| 2 |
∴这圈金属丝的周长最小为2AC=2
| 2 |
故答案为:2
| 2 |
点评:本题考查了平面展开-最短路径问题,圆柱的侧面展开图是一个矩形,此矩形的长等于圆柱底面周长,高等于圆柱的高,本题就是把圆柱的侧面展开成矩形,“化曲面为平面”,用勾股定理解决.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
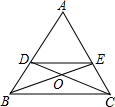 在△ABC中,AB=AC,BE,CD分别是∠ABC,∠ACB的平分线,则下列结论不正确的是( )
在△ABC中,AB=AC,BE,CD分别是∠ABC,∠ACB的平分线,则下列结论不正确的是( )| A、△OBC是等腰三角形 |
| B、△DBE是等腰三角形 |
| C、△DCE是等腰三角形 |
| D、△ACD是等腰三角形 |
函数y=(m+2)xm2-3+(m-2)是关于x的一次函数,则m的值为( )
| A、±2 | B、2 | C、-2 | D、不存在 |
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求(
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,求( 观察函数y=
观察函数y= 如图,已知菱形ABCD中,对角线AC、BD交于O点,AB=10,BD=12,则AC=
如图,已知菱形ABCD中,对角线AC、BD交于O点,AB=10,BD=12,则AC=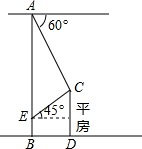 如图,已知楼AB高25米,从楼顶A处测得对面小平房C的俯角为60°,又乘电梯到离地5米的一窗户E处测得小平房顶C的仰角为45°,则小平房到大楼的距离为
如图,已知楼AB高25米,从楼顶A处测得对面小平房C的俯角为60°,又乘电梯到离地5米的一窗户E处测得小平房顶C的仰角为45°,则小平房到大楼的距离为 如图,在直角坐标系平面内有一点P(3,4),求OP与x轴的正半轴的夹角α及y轴的正半轴的夹角β的正切值.
如图,在直角坐标系平面内有一点P(3,4),求OP与x轴的正半轴的夹角α及y轴的正半轴的夹角β的正切值.