题目内容
17.分解因式(1)$\frac{1}{4}$a-a2+a3;
(2)9(x+2)2-25(x-3)2;
(3)(x+1)(x+2)+$\frac{1}{4}$.
分析 (1)直接提取公因式a,进而利用完全平方公式分解因式即可;
(2)直接利用平方差公式分解因式得出答案;
(3)首先去括号,进而利用完全平方公式分解因式即可.
解答 解:(1)$\frac{1}{4}$a-a2+a3=a(a2-a+$\frac{1}{4}$)
=a(a-$\frac{1}{2}$)2;
(2)9(x+2)2-25(x-3)2
=[3(x+2)-5(x-3)][3(x+2)+5(x-3)]
=(-2x+21)(8x-9)
=-(2x-21)(8x-9);
(3)(x+1)(x+2)+$\frac{1}{4}$
=x2+3x+2+$\frac{1}{4}$
=(x+$\frac{3}{2}$)2.
点评 此题主要考查了公式法以及提取公因式分解因式,正确应用公式是解题关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
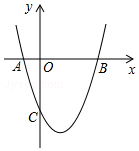 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.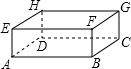 如图,长方体的长、宽、高分别为6cm,5cm,4cm,现有一只蜘蛛由A出发去捕食G处的昆虫,则这只蜘蛛的最短爬行路线的长为3$\sqrt{13}$cm.
如图,长方体的长、宽、高分别为6cm,5cm,4cm,现有一只蜘蛛由A出发去捕食G处的昆虫,则这只蜘蛛的最短爬行路线的长为3$\sqrt{13}$cm.