题目内容
2.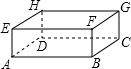 如图,长方体的长、宽、高分别为6cm,5cm,4cm,现有一只蜘蛛由A出发去捕食G处的昆虫,则这只蜘蛛的最短爬行路线的长为3$\sqrt{13}$cm.
如图,长方体的长、宽、高分别为6cm,5cm,4cm,现有一只蜘蛛由A出发去捕食G处的昆虫,则这只蜘蛛的最短爬行路线的长为3$\sqrt{13}$cm.
分析 作此题要把这个长方体中,蚂蚁所走的路线放到一个平面内,在平面内线段最短,根据勾股定理即可计算.
解答 解:第一种情况:把我们所看到的前面和上面组成一个平面,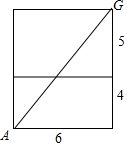
则这个长方形的长和宽分别是9和6,
则所走的最短线段是$\sqrt{{6}^{2}+{9}^{2}}$=3$\sqrt{13}$;
第二种情况:把我们看到的左面与上面组成一个长方形,
则这个长方形的长和宽分别是10和5,
所以走的最短线段是$\sqrt{1{0}^{2}+{5}^{2}}$=5$\sqrt{5}$;
第三种情况:把我们所看到的前面和右面组成一个长方形,
则这个长方形的长和宽分别是11和4,
所以走的最短线段是$\sqrt{1{1}^{2}+{4}^{2}}$=$\sqrt{137}$,
三种情况比较而言,第一种情况最短.
所以爬行的最短路程是3$\sqrt{13}$cm.
故答案为3$\sqrt{13}$cm.
点评 本题考查平面展开路径问题,本题关键知道蚂蚁爬行的路线不同,求出的值就不同,有三种情况,可求出值找到最短路线.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
12.如图,已知∠BAC=∠DAC,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )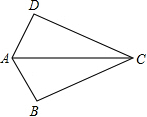

| A. | CB=CD | B. | AB=AD | C. | ∠BCA=∠DCA | D. | ∠B=∠D |
 如图,正方形网格中,已有两个小正方形被涂黑,再涂黑另外一个小正方形,使整个被涂黑的图案构成一个轴对称图形的方法有( )
如图,正方形网格中,已有两个小正方形被涂黑,再涂黑另外一个小正方形,使整个被涂黑的图案构成一个轴对称图形的方法有( )