题目内容
7.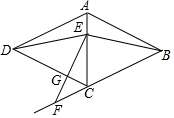 如图,在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,
如图,在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,EF与CD相交于点G;
(1)求证:EG•GF=CG•GD;
(2)联结DF,如果EF⊥CD,那么∠FDC与∠ADC之间有怎样的数量关系?证明你的结论.
分析 (1)先证明△BCE≌△DCE,得∠EDC=∠EBC;利用此条件再证明∠DGE∽△FGC,即可得到EG•GF=CG•GD.
(2)利用第(1)题的结论,可证明△DGE∽△FGC,再利用三角形内角外角关系,即可得到∠ADC与∠FDC的关系.
解答 解:(1)证明:∵点E在菱形ABCD的对角线AC上,
∴∠ECB=∠ECD,
∵BC=CD,CE=CE,
∴△BCE≌△DCE,
∴∠EDC=∠EBC,
∵EB=EF,
∴∠EBC=∠EFC;
∴∠EDC=∠EFC;
∵∠DGE=∠FGC,
∴△DGE∽△FGC;
∴$\frac{EG}{CG}$=$\frac{GD}{FG}$,
∴EG•GF=CG•GD;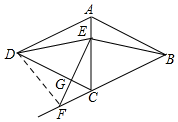
(2)∠ADC=2∠FDC.
证明:∵$\frac{EG}{CG}$=$\frac{GD}{FG}$,
∴$\frac{EG}{DG}$=$\frac{CG}{FG}$,
又∵∠DGF=∠EGC,
∴△CGE∽△FGD,
∵EF⊥CD,DA=DC,
∴∠DAC=∠DCA=∠DFG=90°-∠FDC,
∴∠ADC=180°-2∠DAC=180°-2(90°-∠FDC)=2∠FDC.
点评 本题主要考查了全等三角形的判定及性质、相似三角形的判定及性质、菱形的性质等知识点的综合应用,解题时注意:相似三角形的对应角相等,对应边成比例.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用.

练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
9.对于二次函数y=-$\frac{1}{4}$x2+x-4,下列说法正确的是( )
| A. | 当x>0时,y随x的增大而增大 | B. | 图象的顶点坐标为(-2,-7) | ||
| C. | 当x=2时,y有最大值-3 | D. | 图象与x轴有两个交点 |
2.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{63}$ | B. | $\sqrt{20}$ | C. | $\sqrt{0.2}$ | D. | $\sqrt{21}$ |
17.若关于x的方程kx2+(k+1)x+1=0有两个相等的实数根,则次方程的解为( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
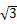 B. 1 C.
B. 1 C. 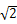 D. 2
D. 2