题目内容
19.已知25x2-144=0,且x>0,求2$\sqrt{5x+13}$的平方根.分析 由25x2-144=0,可求出x的值,根据x的取值范围,把合适的x的值代入2$\sqrt{5x+13}$中,再求2$\sqrt{5x+13}$的平方根.
解答 解:由25x2-144=0,
得x=±$\frac{12}{5}$,
∵x>0,
∴x=$\frac{12}{5}$.
∴2$\sqrt{5x+13}$
=2$\sqrt{5×\frac{12}{5}+13}$
=2×5=10.
∴2$\sqrt{5x+13}$的平方根是$±\sqrt{10}$.
点评 本题考查了平方根求法和平方根的意义,利用平方根的意义求出x的值是解决本题的关键.

练习册系列答案
相关题目
10.下列运算正确的是( )
| A. | (-2ab)•(-3ab)2=-54a4b4 | B. | 5x2•(3x3)2=15x12 | ||
| C. | (-0.1b)•(-10b2)3=-b7 | D. | (2×10a)($\frac{1}{2}$×10a)=102a |
14.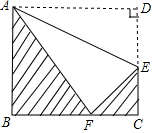 如图,将长方形纸片ABCD沿直线AE折叠,顶点D恰好落在BC边上点F处,已知CE=3cm,AB=8cm,图中阴影部分的面积是( )
如图,将长方形纸片ABCD沿直线AE折叠,顶点D恰好落在BC边上点F处,已知CE=3cm,AB=8cm,图中阴影部分的面积是( )
 如图,将长方形纸片ABCD沿直线AE折叠,顶点D恰好落在BC边上点F处,已知CE=3cm,AB=8cm,图中阴影部分的面积是( )
如图,将长方形纸片ABCD沿直线AE折叠,顶点D恰好落在BC边上点F处,已知CE=3cm,AB=8cm,图中阴影部分的面积是( )| A. | 80cm2 | B. | 50cm2 | C. | 30cm2 | D. | 20cm2 |
8.如果(a-1)x2+ax+a2-1=0是关于x的一元二次方程,那么必有( )
| A. | a≠0 | B. | a≠1 | C. | a≠-1 | D. | a=±-1 |
9.若a2-2a-2=0,则(a-1)2=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
 则这列数的第6个数是( )
则这列数的第6个数是( ) B.
B.  C.
C.  D.
D. 
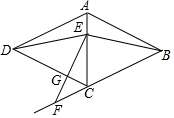 如图,在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,
如图,在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,