题目内容
15.探究与发现: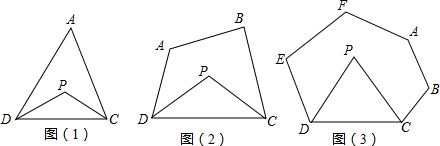
(1)探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系
已知:如图1,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系,并说明理由.
(2)探究二:四边形的两个个内角与另两个内角的平分线所夹的角之间的关系
已知:如图2,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)探究三:六边形的四个内角与另两个内角的平分线所夹的角之间的关系
已知:如图3,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:∠P=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°.
分析 探究一:根据角平分线的定义可得∠PDC=$\frac{1}{2}$∠ADC,∠PCD=$\frac{1}{2}$∠ACD,然后根据三角形内角和定理列式整理即可得解;
探究二:根据四边形的内角和定理表示出∠ADC+∠BCD,然后同理探究二解答即可;
探究三:根据六边形的内角和公式表示出∠EDC+∠BCD,然后同理探究二解答即可.
解答 解:探究一:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=$\frac{1}{2}$∠ADC,∠PCD=$\frac{1}{2}$∠ACD,
∴∠DPC=180°-∠PDC-∠PCD,
=180°-$\frac{1}{2}$∠ADC-$\frac{1}{2}$∠ACD,
=180°-$\frac{1}{2}$(∠ADC+∠ACD),
=180°-$\frac{1}{2}$(180°-∠A),
=90°+$\frac{1}{2}$∠A;
探究二:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=$\frac{1}{2}$∠ADC,∠PCD=$\frac{1}{2}$∠BCD,
∴∠DPC=180°-∠PDC-∠PCD,
=180°-$\frac{1}{2}$∠ADC-$\frac{1}{2}$∠BCD,
=180°-$\frac{1}{2}$(∠ADC+∠BCD),
=180°-$\frac{1}{2}$(360°-∠A-∠B),
=$\frac{1}{2}$(∠A+∠B);
探究三:六边形ABCDEF的内角和为:(6-2)•180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC=$\frac{1}{2}$∠EDC,∠PCD=$\frac{1}{2}$∠BCD,
∴∠P=180°-∠PDC-∠PCD,
=180°-$\frac{1}{2}$∠EDC-$\frac{1}{2}$∠BCD,
=180°-$\frac{1}{2}$(∠EDC+∠ACD),
=180°-$\frac{1}{2}$(720°-∠A-∠B-∠E-∠F),
=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°,
即∠P=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°.
故答案为:∠P=$\frac{1}{2}$(∠A+∠B+∠E+∠F)-180°.
点评 本题考查了三角形的外角性质,三角形的内角和定理,多边形的内角和公式,此类题目根据同一个解答思路求解是解题的关键.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案| A. | 223×104 | B. | 0.223×107 | C. | 2.23×106 | D. | 2.23×107 |
| A. | (-2ab)•(-3ab)2=-54a4b4 | B. | 5x2•(3x3)2=15x12 | ||
| C. | (-0.1b)•(-10b2)3=-b7 | D. | (2×10a)($\frac{1}{2}$×10a)=102a |
| A. | -3 | B. | -1 | C. | 1 | D. | 5 |
| A. | 一条直线可以看成一个平角 | |
| B. | 周角是一条射线 | |
| C. | 角是由一条射线旋转而成的 | |
| D. | 角是由公共端点的两条射线组成的图形 |
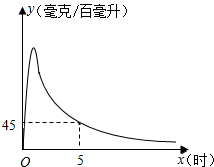 如图,实验数据显示,一般成年人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可以近似的用二次函数y=-200x2+400x刻画,1.5小时后(包括1.5小时)y与x可近似的用反比例函数y=$\frac{k}{x}$(k>0)刻画.
如图,实验数据显示,一般成年人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可以近似的用二次函数y=-200x2+400x刻画,1.5小时后(包括1.5小时)y与x可近似的用反比例函数y=$\frac{k}{x}$(k>0)刻画.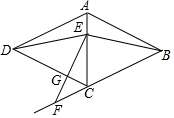 如图,在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,
如图,在菱形ABCD中,点E在对角线AC上,点F在BC的延长线上,EF=EB,