题目内容
13.若$\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=k$(k≠0),则分式$\frac{3a+4b-5c}{2b-4a+c}$=0.分析 用k表示出a、b、c,然后代入比例式进行计算即可得解.
解答 解:∵$\frac{a}{3}$=$\frac{b}{4}$=$\frac{c}{5}$=k,
∴a=3k,b=4k,c=5k,
∴$\frac{3a+4b-5c}{2b-4a+c}$=$\frac{3•3k+4•4k-5•5k}{2•4k-4•3k+5k}$=$\frac{0}{k}$=0.
故答案为:0.
点评 本题考查了比例的性质,用k分别表示出a、b、c是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
4. 已知某一次函数y=kx+b的图象如图所示,则k、b的值可能是( )
已知某一次函数y=kx+b的图象如图所示,则k、b的值可能是( )
 已知某一次函数y=kx+b的图象如图所示,则k、b的值可能是( )
已知某一次函数y=kx+b的图象如图所示,则k、b的值可能是( )| A. | k=-$\frac{3}{2}$,b=3 | B. | k=-$\frac{3}{2}$,b=-3 | C. | k=$\frac{3}{2}$,b=3 | D. | k=$\frac{3}{2}$,b=-3 |
1.已知$\frac{a}{b}$=$\frac{c}{d}$=$\frac{2}{5}$(b≠0.5d),则$\frac{2a-c}{2b-d}$等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{5}$ |
2.若分式$\frac{{x}^{2}-4x+3}{|x|-1}$的值为零,则x的值是( )
| A. | 3 | B. | 1 | C. | 1或3 | D. | -1 |
16.如果m=$\sqrt{11}$-2,那么m的取值范围是( )
| A. | 0<m<1 | B. | 1<m<2 | C. | 2<m<3 | D. | 3<m<4 |
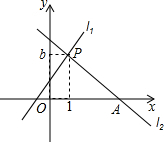 如图,直线l1:y=x+1与直线l2:y=mx+n交于点P(1,b),直线l2与x轴交于点A(4,0).
如图,直线l1:y=x+1与直线l2:y=mx+n交于点P(1,b),直线l2与x轴交于点A(4,0). 如图,直线 DE∥BC,射线AB、AG、AC分别交DE、BC于D、F、E和B、G、C,试说明$\frac{DF}{BG}=\frac{FE}{GC}$.
如图,直线 DE∥BC,射线AB、AG、AC分别交DE、BC于D、F、E和B、G、C,试说明$\frac{DF}{BG}=\frac{FE}{GC}$.