题目内容
17.如果一元二次方程ax2+bx+c=0(a≠0)满足a+b+c=0,那么我们称这个方程为“凤凰”方程,已知ax2+bx+c=0(a≠0)是“凤凰”方程,且有一个解为-1,则下列结论正确的是( )| A. | a=c,b=1 | B. | a=b,c=0 | C. | a=-c,b=0 | D. | a=b=c |
分析 根据凤凰方程的定义及方程有个解为-1即可得到答案.
解答 解:∵已知ax2+bx+c=0(a≠0)是“凤凰”方程,且有一个解为-1,
∴$\left\{\begin{array}{l}{a+b+c=0}\\{a-b+c=0}\end{array}\right.$,
∴a+c=0,b=0,
即a=-c,b=0,
故选C.
点评 此题考查了一元二次方程的解的知识,解题的关键是了解凤凰方程的定义,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.若分式$\frac{{x}^{2}-4x+3}{|x|-1}$的值为零,则x的值是( )
| A. | 3 | B. | 1 | C. | 1或3 | D. | -1 |
19. 如图,在五边形ABCDE中,∠A+∠B+∠E=α,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )
如图,在五边形ABCDE中,∠A+∠B+∠E=α,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )
 如图,在五边形ABCDE中,∠A+∠B+∠E=α,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )
如图,在五边形ABCDE中,∠A+∠B+∠E=α,DP、CP分别平分∠EDC、∠BCD,则∠P的度数是( )| A. | $\frac{1}{2}$α-90° | B. | 90°$+\frac{1}{2}α$ | C. | $\frac{1}{2}α$ | D. | 540°$-\frac{1}{2}α$ |

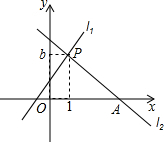 如图,直线l1:y=x+1与直线l2:y=mx+n交于点P(1,b),直线l2与x轴交于点A(4,0).
如图,直线l1:y=x+1与直线l2:y=mx+n交于点P(1,b),直线l2与x轴交于点A(4,0).