题目内容
8.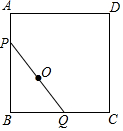 如图,以AB为边作正方形ABCD,动点P、Q分别在AB和BC边上运动,且PQ=AB=8,若点Q从点B出发,沿BC向点C运动,则点P随之沿AB下滑,当B到达C点时停止运动.则点Q从B到C的运动过程中,PQ的中点O所经过的路径长为2π.
如图,以AB为边作正方形ABCD,动点P、Q分别在AB和BC边上运动,且PQ=AB=8,若点Q从点B出发,沿BC向点C运动,则点P随之沿AB下滑,当B到达C点时停止运动.则点Q从B到C的运动过程中,PQ的中点O所经过的路径长为2π.
分析 连结BO,则OB=$\frac{1}{2}$PQ=4,故此点O在以B为圆心以BO为半径的圆上,最后依据扇形的弧长公式求解即可.
解答 解:如图所示:连结OB.
∵O是PQ的中点,
∴OB=$\frac{1}{2}$PQ=4.
又∵当点P与点A重合时,点O在AB上,当点P与点B重合时,点O在BC上,
∴点O在以B为以B为圆心以BO为半径的圆上且扇形的圆心角为90°.
∴点O运动的路线长=$\frac{90π×4}{180}$=2π.
故答案为:2π.
点评 本题主要考查的是动点的轨迹、扇形的弧长公式、直角三角三角形的性质,判断出点O的轨迹的形状是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.若$\left\{\begin{array}{l}{x=-3}\\{y=2}\end{array}\right.$是$\left\{\begin{array}{l}{αx+θy=1}\\{θx-βy=-2}\end{array}\right.$的解,则α、β之间的关系是( )
| A. | β-9α=1 | B. | 9α+4β=1 | C. | 3α+2β=1 | D. | 4β-9α+1=0 |
 如图,BD是△ABC的角平分线,它的垂直平分线分别交AB、BC于点E、F、G,连接ED、DG.
如图,BD是△ABC的角平分线,它的垂直平分线分别交AB、BC于点E、F、G,连接ED、DG. 如图,已知△OAA1是腰长为1的等腰直角三角形,以Rt△OAA1的斜边AA1为直角边,画第二个等腰直角三角形AA1A2,再以Rt△AA1A2的斜边AA2为直角边,画第三个等腰直角气角形AA2A3…依此类推,则点A2016的坐标是(-21008+1,0).
如图,已知△OAA1是腰长为1的等腰直角三角形,以Rt△OAA1的斜边AA1为直角边,画第二个等腰直角三角形AA1A2,再以Rt△AA1A2的斜边AA2为直角边,画第三个等腰直角气角形AA2A3…依此类推,则点A2016的坐标是(-21008+1,0).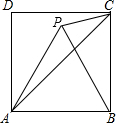 如图,四边形ABCD是边长为4的正方形,△ABP是等边三角形,则△APC的面积是4$\sqrt{3}$-4.
如图,四边形ABCD是边长为4的正方形,△ABP是等边三角形,则△APC的面积是4$\sqrt{3}$-4.