题目内容
如图,每个大正方形是由边长为1的小正方形组成.观察如图图形,完成下列填空:
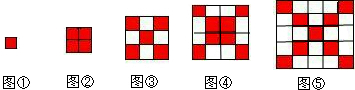
(1)猜想:当n为奇数时,图n中黑色小正方形的个数为 ,当n为偶数时,图n中黑色小正方形的个数为 ;
(2)在边长为偶数的正方形中,白色小正方形的个数是黑色小正方形个数的4倍,求这个正方形的边长.

(1)猜想:当n为奇数时,图n中黑色小正方形的个数为
(2)在边长为偶数的正方形中,白色小正方形的个数是黑色小正方形个数的4倍,求这个正方形的边长.
考点:一元二次方程的应用,规律型:图形的变化类
专题:应用题
分析:(1)当n为奇数时,图n中黑色小正方形的个数为第n个奇数,当n为偶数时,图n中黑色小正方形的个数为第n个偶数;
(2)设这个正方形的边长为n,根据题意列出关于n的方程,求出方程的解即可得到n的值.
(2)设这个正方形的边长为n,根据题意列出关于n的方程,求出方程的解即可得到n的值.
解答:解:(1)当n为奇数时,图n中黑色小正方形的个数为2n-1,当n为偶数时,图n中黑色小正方形的个数为2n;
故答案为:2n-1;2n;
(2)设这个正方形的边长为n,
根据题意,得n2-2n=4×2n,
整理得:n2-10n=0,
解得:n=10或n=0(不合题意,舍去)
答:这个正方形的边长为10.
故答案为:2n-1;2n;
(2)设这个正方形的边长为n,
根据题意,得n2-2n=4×2n,
整理得:n2-10n=0,
解得:n=10或n=0(不合题意,舍去)
答:这个正方形的边长为10.
点评:此题考查了一元二次方程的应用,以及规律型:数字得变化类,弄清题意是解本题的关键.

练习册系列答案
相关题目
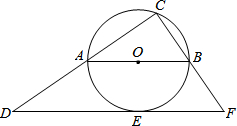 如图,AB为⊙O的直径,C为⊙O上一点,DF切⊙O于E点,分别与CA、CB的延长线于点D、F,已知AB∥DF,CD=4,CF=3,则AC=( )
如图,AB为⊙O的直径,C为⊙O上一点,DF切⊙O于E点,分别与CA、CB的延长线于点D、F,已知AB∥DF,CD=4,CF=3,则AC=( )A、
| ||
B、
| ||
C、
| ||
D、
|

 在正方形网格中建立如图的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题:
在正方形网格中建立如图的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标是(4,4),请解答下列问题: 如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,连接OD,过点D作⊙O的切线,交AB延长线于点E,交AC于点F.
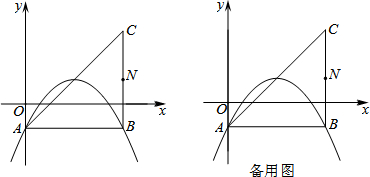
如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,连接OD,过点D作⊙O的切线,交AB延长线于点E,交AC于点F. 如图,一只碗,从侧面观察碗身是一条抛物线,而俯视又是一个圆,已知碗深为5cm,碗口宽为10cm,现向碗中加水,使它刚好漂浮四张半径均为2cm的圆形薄纸片,则加入的水深应是多少?
如图,一只碗,从侧面观察碗身是一条抛物线,而俯视又是一个圆,已知碗深为5cm,碗口宽为10cm,现向碗中加水,使它刚好漂浮四张半径均为2cm的圆形薄纸片,则加入的水深应是多少?