题目内容
20.已知关于x的一元二次方程x2+3x+1-m=0有两个不相等的实数根.(1)求m的取值范围;
(2)若m为负整数,求此时方程的根.
分析 (1)由方程有两个不等实数根可得b2-4ac>0,代入数据即可得出关于m的一元一次不等式,解不等式即可得出结论;
(2)根据m为负整数以及(1)的结论可得出m的值,将其代入原方程,利用分解因式法解方程即可得出结论.
解答 解:(1)∵关于x的一元二次方程x2+3x+1-m=0有两个不相等的实数根,
∴△=b2-4ac=32-4(1-m)>0,
即5+4m>0,解得:m>-$\frac{5}{4}$.
∴m的取值范围为m>-$\frac{5}{4}$.
(2)∵m为负整数,且m>-$\frac{5}{4}$,
∴m=-1.
将m=-1代入原方程得:x2+3x+2=(x+10)(x+2)=0,
解得:x1=-1,x2=-2.
故当m=-1时,此方程的根为x1=-1和x2=-2.
点评 本题考查了根的判别式、解一元一次不等式以及用因式分解法解方程,解题的关键:(1)由根的情况得出关于m的一元一次不等式;(2)确定m的值.本题属于基础题,难度不大,解决该题型题目时,由方程根的个数结合根的判别式得出不等式(或不等式组)是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
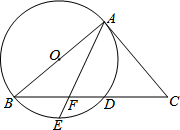 如图,以△ABC的边AB为直径作⊙O,与BC交于点D,点E是弧BD的中点,连接AE交BC于点F,∠ACB=2∠BAE.
如图,以△ABC的边AB为直径作⊙O,与BC交于点D,点E是弧BD的中点,连接AE交BC于点F,∠ACB=2∠BAE.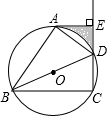 如图,BD是⊙O的直径,点A、C在⊙O上,过点A作⊙O的切线AE交CD的延长线于点E,且DA平分∠BDE.
如图,BD是⊙O的直径,点A、C在⊙O上,过点A作⊙O的切线AE交CD的延长线于点E,且DA平分∠BDE. 如图,直线a、b被c所截,∠1-∠2=11°,∠3+∠4=169°,求∠1和∠2的度数.[方法提示:注意邻补角].
如图,直线a、b被c所截,∠1-∠2=11°,∠3+∠4=169°,求∠1和∠2的度数.[方法提示:注意邻补角].