题目内容
5.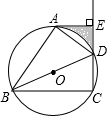 如图,BD是⊙O的直径,点A、C在⊙O上,过点A作⊙O的切线AE交CD的延长线于点E,且DA平分∠BDE.
如图,BD是⊙O的直径,点A、C在⊙O上,过点A作⊙O的切线AE交CD的延长线于点E,且DA平分∠BDE.(1)求证:AE⊥CD;
(2)若⊙O的半径为1cm,∠EAD=30°,求图中阴影部分的面积;
(3)第(2)问中的解题过程,用到的数学思想是转化的思想.
分析 (1)欲证明AE⊥CD,只要证明∠EAD+∠ADE=90°即可.
(2)根据S阴=S四边形AEDO-S扇形OAD=S△AED+S△AOD-S扇形OAD计算即可.
(3)把求不规则图形面积转化为求规则图形面积去思考,体现了转化的思想.
解答 (1)证明: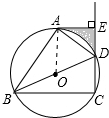 连接OA.
连接OA.
∵AE是⊙O切线,
∴OA⊥AE,
∴∠OAE=90°,
∴∠EAD+∠OAD=90°,
∵∠ADO=∠ADE,OA=OD,
∴∠OAD=∠ODA=∠ADE,
∴∠EAD+∠ADE=90°,
∴∠AED=90°,
∴AE⊥CD.
(2)解:∵∠EAD=30°,∠AED=90°,
∴∠ADE=∠ADO=∠OAD=60°,
∴∠AOD=60°,
∴S阴=S四边形AEDO-S扇形OAD=S△AED+S△AOD-S扇形OAD=$\frac{1}{2}$•$\frac{\sqrt{3}}{2}$$•\frac{1}{2}$+$\frac{\sqrt{3}}{4}$-$\frac{60π•{1}^{2}}{360}$=$\frac{3\sqrt{3}}{8}$-$\frac{π}{6}$.
(3)第(2)问中的解题过程,用到的数学思想是转化的思想.
故答案为转化的思想.
点评 本题考查切线的性质、扇形的面积、三角形的面积等知识,解题的关键是熟练掌握切线的性质,学会添加常用辅助线,属于中考常考题型.

练习册系列答案
相关题目
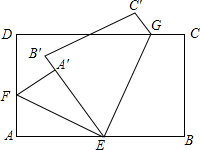 如图,将长方形绒片折叠,折痕为EF和EG,点A落在A处,点B落在B′处,且EA′和EB′重合.
如图,将长方形绒片折叠,折痕为EF和EG,点A落在A处,点B落在B′处,且EA′和EB′重合.