题目内容
8.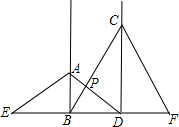 如图,工地上竖立着两根电线杆AB、CD,它们相距15m,分别自两杆上高出地面4m、6m的A、C处,向两侧地面上的E和D、B和F处用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD与BC的交点P离地面的高度PH是多少米?
如图,工地上竖立着两根电线杆AB、CD,它们相距15m,分别自两杆上高出地面4m、6m的A、C处,向两侧地面上的E和D、B和F处用钢丝绳拉紧,以固定电线杆,那么钢丝绳AD与BC的交点P离地面的高度PH是多少米?
分析 可过点P作PQ⊥BD于Q,由平行线分线段成比例可得$\frac{h}{4}$=$\frac{y}{x+y}$及$\frac{h}{6}$=$\frac{x}{x+y}$,进而即可得出PQ的长.
解答  解:作PQ⊥BD于Q,设BQ=x米,QD=y米,PQ=h米,
解:作PQ⊥BD于Q,设BQ=x米,QD=y米,PQ=h米,
∵AB∥PQ∥CD,
∴$\frac{PQ}{AB}$=$\frac{BQ}{BD}$,$\frac{PQ}{CD}$=$\frac{BQ}{BD}$,
即$\frac{h}{4}$=$\frac{y}{x+y}$及$\frac{h}{6}$=$\frac{x}{x+y}$,
∴两式相加得$\frac{5h}{12}$=1,
由此得h=2.4米.
即点P离地面的高度为2.4米.
点评 本题主要考查了平行线分线段成比例的性质问题,解题的关键是能从实际问题中整理出相似三角形,应能够熟练运用.

练习册系列答案
相关题目
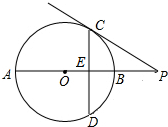 如图,AB是⊙O的直径,P是AB延长线上一点,PC切⊙O于C,作C关于AP的对称点D,连接CD交AB于E,且AB=6,OE=1,则PC=6$\sqrt{2}$.
如图,AB是⊙O的直径,P是AB延长线上一点,PC切⊙O于C,作C关于AP的对称点D,连接CD交AB于E,且AB=6,OE=1,则PC=6$\sqrt{2}$.
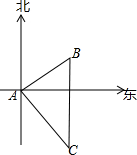 甲、乙两船同时从A港出发,甲以12n mile/h的速度沿北偏东50°方向航行,乙以16n mi1e/h的速度沿南偏东方向航行.3h后,甲、乙两船分别位于B,C处,且相距60n mi1e,求乙船航行的具体方向.
甲、乙两船同时从A港出发,甲以12n mile/h的速度沿北偏东50°方向航行,乙以16n mi1e/h的速度沿南偏东方向航行.3h后,甲、乙两船分别位于B,C处,且相距60n mi1e,求乙船航行的具体方向.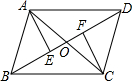 如图,在?ABCD中,AC与BD相交于点O,AE⊥BD于E,AF⊥BD于F,则图中的全等三角形共有6对.
如图,在?ABCD中,AC与BD相交于点O,AE⊥BD于E,AF⊥BD于F,则图中的全等三角形共有6对.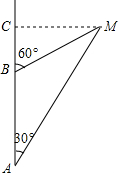 钓鱼岛自古就是中国的领土,中国有关部门己钓鱼岛及其附属岛屿开展常态化监视监测,一日,中国一艘海监船从A点沿正北方向以每小时24海里的速度巡航,在A点测得钓鱼岛中心M在点A的北偏东30°方向,问航行半小时后到达B点,测得钓鱼岛中心M在点B的北偏东60°方向,问再航行多少小时距离钓鱼岛中心最近?
钓鱼岛自古就是中国的领土,中国有关部门己钓鱼岛及其附属岛屿开展常态化监视监测,一日,中国一艘海监船从A点沿正北方向以每小时24海里的速度巡航,在A点测得钓鱼岛中心M在点A的北偏东30°方向,问航行半小时后到达B点,测得钓鱼岛中心M在点B的北偏东60°方向,问再航行多少小时距离钓鱼岛中心最近?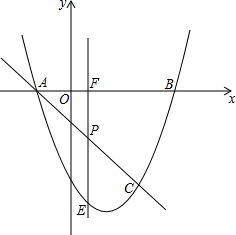 如图所示,抛物线y=x2-3x-4与x轴交于A,B两点(A点在B点左侧),直线y=kx-1与抛物线y=x2-3x-4交于A,C两点.求A,B,C三点的坐标.
如图所示,抛物线y=x2-3x-4与x轴交于A,B两点(A点在B点左侧),直线y=kx-1与抛物线y=x2-3x-4交于A,C两点.求A,B,C三点的坐标.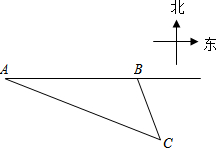 如图,我渔政船在东海海面上自西向东匀速巡航,在A地观测到某海岛C在东偏南21.3°方向上.若渔政船继续向东航行60海里到达B处,此时观测到海岛C在东偏南63.5°方向上.之后,渔政船再向东航多少海里,离海岛C的距离最近?
如图,我渔政船在东海海面上自西向东匀速巡航,在A地观测到某海岛C在东偏南21.3°方向上.若渔政船继续向东航行60海里到达B处,此时观测到海岛C在东偏南63.5°方向上.之后,渔政船再向东航多少海里,离海岛C的距离最近?