题目内容
4.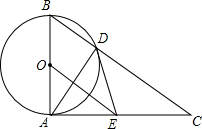 如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.
如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.(1)求证:ED是⊙O的切线.
(2)当OA=3,OE=6时,求线段AE、线段DE和弧AD围成的图形的面积.
分析 (1)如图,连接OD.通过证明△AOE≌△DOE得到∠OAE=∠ODE=90°,易证得结论;
(2)在Rt△OAE中,由OA=3,OE=6,得出cos∠AOE=$\frac{1}{2}$,得出∠AOE=60°,进而求得AE的长和∠AOD=120°,然后根据S四边形OAED-S扇形OAD即可求得线段AE、线段DE和弧AD围成的图形的面积.
解答 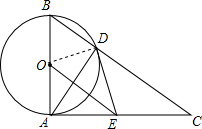 (1)证明:如图,连接OD.
(1)证明:如图,连接OD.
∵AC⊥AB,
∴∠BAC=90°,即∠OAE=90°.
在△AOE与△DOE中,
$\left\{\begin{array}{l}{OA=OD}\\{OE=OE}\\{AE=DE}\end{array}\right.$,
∴△AOE≌△DOE(SSS),
∴∠OAE=∠ODE=90°,即OD⊥ED.
又∵OD是⊙O的半径,
∴ED是⊙O的切线;
(2)解:如图,在Rt△OAE中,OA=3,OE=6,
∴$cos∠AOE=\frac{3}{6}=\frac{1}{2}$,
∴∠AOE=60°,
∴∠AOD=120°,AE=OE•sin∠AOE=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
∴S△AOE=$\frac{1}{2}$AE•OA=$\frac{1}{2}$×3$\sqrt{3}$×3=$\frac{9\sqrt{3}}{2}$,
∴S四边形OAED=2S△AOE=9$\sqrt{3}$,
∴线段AE、线段DE和弧AD围成的图形的面积=S四边形OAED-S扇形OAD
=9$\sqrt{3}$-$\frac{120π×{3}^{2}}{360}$
=9$\sqrt{3}$-3π.
点评 本题考查了切线的判定以及扇形的面积,求得△AOE≌△DOE和∠AOE=60°是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
12.若方程组$\left\{\begin{array}{l}{2a-3b=13}\\{3a+5b=30}\end{array}\right.$的解是$\left\{\begin{array}{l}{a=8.3}\\{b=1.2}\end{array}\right.$,则方程组$\left\{\begin{array}{l}{2(x+2)-3(y-1)=13}\\{3(x+2)+5(y-1)=30}\end{array}\right.$的解是( )
| A. | $\left\{\begin{array}{l}{x=8.3}\\{y=1.2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=10.3}\\{y=1.2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=6.3}\\{y=2.2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=10.3}\\{y=0.2}\end{array}\right.$ |
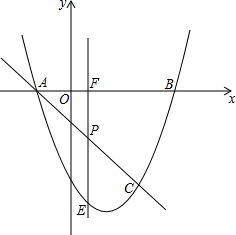 如图所示,抛物线y=x2-3x-4与x轴交于A,B两点(A点在B点左侧),直线y=kx-1与抛物线y=x2-3x-4交于A,C两点.求A,B,C三点的坐标.
如图所示,抛物线y=x2-3x-4与x轴交于A,B两点(A点在B点左侧),直线y=kx-1与抛物线y=x2-3x-4交于A,C两点.求A,B,C三点的坐标. 由一些大小相同、边长为1cm的小正方形组成的几何体的三视图如图所示,那么这个几何体表面积是22cm2,体积是5cm3.
由一些大小相同、边长为1cm的小正方形组成的几何体的三视图如图所示,那么这个几何体表面积是22cm2,体积是5cm3.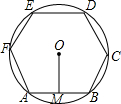 已知⊙O的内接正六边形ABCDEF的边心距OM为$\sqrt{3}$cm,则的⊙O半径为2cm.
已知⊙O的内接正六边形ABCDEF的边心距OM为$\sqrt{3}$cm,则的⊙O半径为2cm.
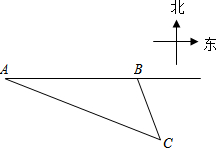 如图,我渔政船在东海海面上自西向东匀速巡航,在A地观测到某海岛C在东偏南21.3°方向上.若渔政船继续向东航行60海里到达B处,此时观测到海岛C在东偏南63.5°方向上.之后,渔政船再向东航多少海里,离海岛C的距离最近?
如图,我渔政船在东海海面上自西向东匀速巡航,在A地观测到某海岛C在东偏南21.3°方向上.若渔政船继续向东航行60海里到达B处,此时观测到海岛C在东偏南63.5°方向上.之后,渔政船再向东航多少海里,离海岛C的距离最近?