题目内容
2．函数y=-$\frac{6}{x}$的图象经过点A（x1，y1）、B（x2，y2），若x1＜x2＜0，则y1、y2、0三者的大小关系是（ ）| A． | y1＜y2＜0 | B． | y2＜y1＜0 | C． | y1＞y2＞0 | D． | y2＞y1＞0 |
分析 根据反比例函数图象上点的坐标特征得到x1•y1=x2•y2=-6，然后根据x1＜x2＜0即可得到y1与y2的大小关系．
解答 解：根据题意得x1•y1=x2•y2=-6，
而x1＜x2＜0，
∴0＜y1＜y2．
故选D．
点评 本题考查了反比例函数图象上点的坐标特征：反比例函数y=$\frac{k}{x}$（k为常数，k≠0）的图象是双曲线，图象上的点（x，y）的横纵坐标的积是定值k，即xy=k．
练习册系列答案
相关题目
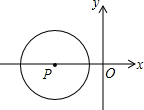如图，平面直角坐标中，半径为2的⊙P的圆心P的坐标为（-3，0），将⊙P沿x轴正方向平移，使⊙P与y轴相交，则平移的距离d的取值范围是1＜d＜5．
10．计算$\sqrt{12}×\sqrt{\frac{1}{3}}+\sqrt{5}×\sqrt{3}$的结果在（ ）
| A． | 4至5之间 | B． | 5至6之间 | C． | 6至7之间 | D． | 7至8之间 |
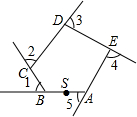如图，五边形ABCDE是一块草地．小明从点S出发，沿着这个五边形的边步行一周，最后仍回到起点S处，小明在各拐弯处转过的角度之和是360°．
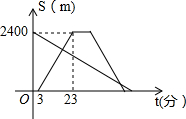小红从劳动基地出发，步行返回学校，小军骑车从学校出发去劳动基地，在基地停留10分钟后，沿原路以原速返回，结果比小红早7分钟回到学校，若两人都是沿着同一路线行进，且两人与学校的距离s（米）和小红从劳动基地出发所用时间t（分）之间的函数关系如图所示，则下列说法中正确的结论有（ ）个
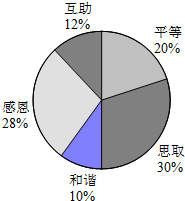某校开展了以“人生观、价值观”为主题的班会活动，活动结束后，初三（1）班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查（要求每位同学只选自己最认可的一项观点），并制成了如下扇形统计图．