Question

11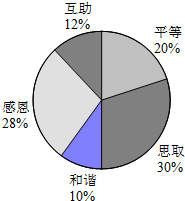．某校开展了以“人生观、价值观”为主题的班会活动，活动结束后，初三（1）班数学兴趣小组提出了5个主要观点并在本班50名学生中进行了调查（要求每位同学只选自己最认可的一项观点），并制成了如下扇形统计图．
（1）该班学生选择“和谐”观点的有5人，在扇形统计图中，“和谐”观点所在扇形区域的圆心角是36°
（2）如果该校有400名初三学生，利用样本估计选择“感恩”观点的初三学生约有112人．
（3）如果数学兴趣小组在这5个主要观点中任选两项观点在全校学生中进行调查，求恰好选到“和谐”和“感恩”观点的概率．（用树状图或列表法分析解答）

Answer 1

分析 （1）由扇形统计图可求得该班学生选择“和谐”观点的学生数，求得“和谐”观点所在扇形区域的圆心角度数；
（2）由选择“感恩”观点的初三学生占28%，即可求得答案；
（3）首先根据题意列出表格，然后由表格即可求得所有等可能的结果与恰好选到“和谐”和“感恩”观点的情况，再利用概率公式即可求得答案．

解答 解：（1）该班学生选择“和谐”观点的有：50×10%=5（人）；“和谐”观点所在扇形区域的圆心角是：360°×10%=36°；
故答案为：5，36；

（2）选择“感恩”观点的初三学生约有：400×28%=112（人）；
故答案为：112；

（3）列表法得：

	平等	进取	和谐	感恩	互助
平等		平等、进取	平等、和谐	平等、感恩	平等、互助
进取	进取、平等		进取、和谐	进取、感恩	进取、互助
和谐	和谐、平等	和谐、进取		和谐、感恩	和谐、互助
感恩	感恩、平等	感恩、进取	感恩、和谐		感恩、互助
互助	互助、平等	互助、进取	互助、和谐	互助、感恩

∵共有20种等可能的结果，恰好选到“和谐”和“感恩”观点的有2种情况，
∴恰好选到“和谐”和“感恩”观点的概率是：$\frac{1}{10}$．

点评 此题考查了列表法或树状图法求概率以及扇形统计图的知识．用到的知识点为：概率=所求情况数与总情况数之比．